Topic Question Set
Q 21
:
Let the shortest distance from (a, 0), a > 0, to the parabola be 4. Then the equation of the circle passing through the point (a, 0) and the focus of the parabola, and having its centre on the axis of the parabola is: [2025]
(4)
Equation of normal at is given by
... (i)
Put x = a, y = 0 in equation (i), we get
The point Q is
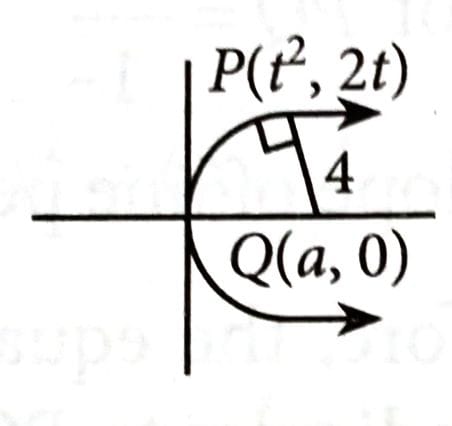
Focus of parabola is (1, 0) and centre of circle lie on axis of parabola.
(1, 0) and (5, 0) will be the end points of diameter of the circle.
Equation of circle is
.
Q 22
:
If the equation of the parabola with vertex and the directrix x + 2y = 0 is , then is equal to : [2025]
9
6
8
7
(1)
Given : Vertex of parabola and directrix is x + 2y = 0
Since, axis is to directrix and passes through vertex, then equation of axis
Foot of directrix is intersecting point of
y = 2x & 2y + x = 0 i.e., (0, 0)
Focus (3, 6)
Using definition of parabola,
On comparing we get
Hence, = 4 + 1 + 4 = 9.
Q 23
:
Let ABCD be a trapezium whose vertices lie on the parabola . Let the sides AD and BC of the trapezium be parallel to y-axis. If the diagonal AC is of length and it passes through the point (1, 0), then the area of ABCD is [2025]
(3)
Let and be the points lies on parabola .
Length of (Given)
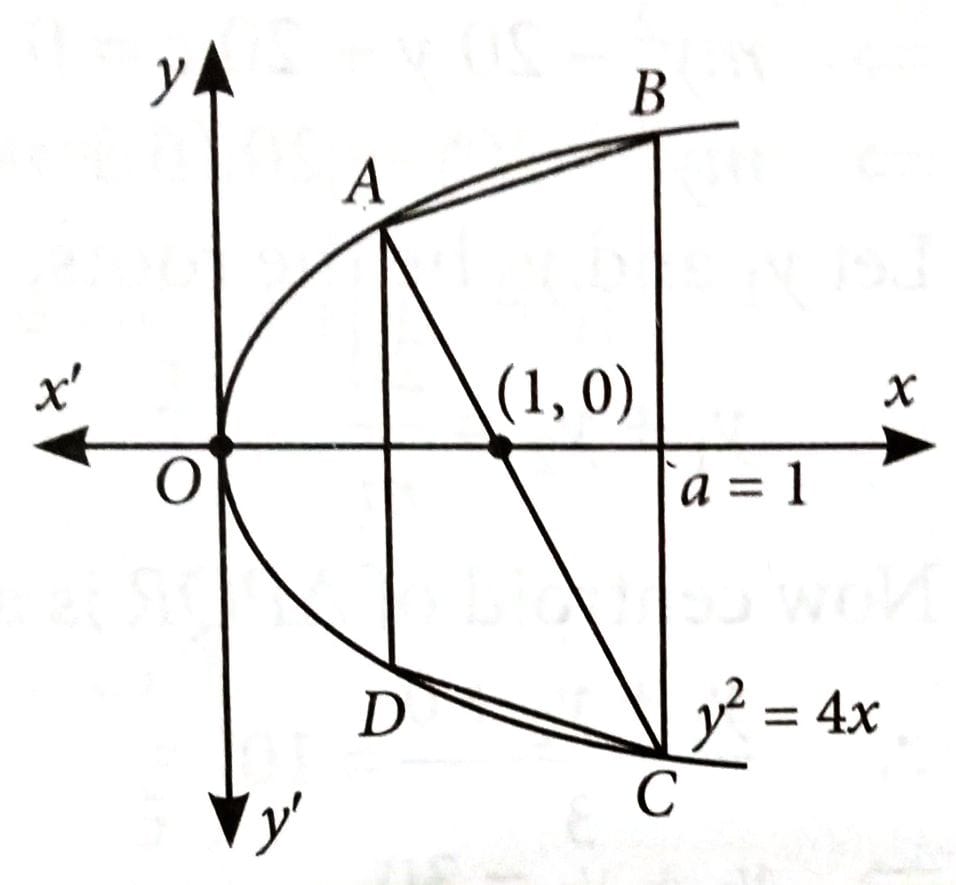
So, and
The area of trapezium ABCD = .
Q 24
:
Two parabolas have the same focus (4, 3) and their directrices are the x-axis and the y-axis, respectively. If these parabolas intersects at the points A and B, then is equal to : [2025]
392
96
384
192
(4)
Let the two parabolas intersect at and .
Equation of parabolas are
... (i)
and ... (ii)
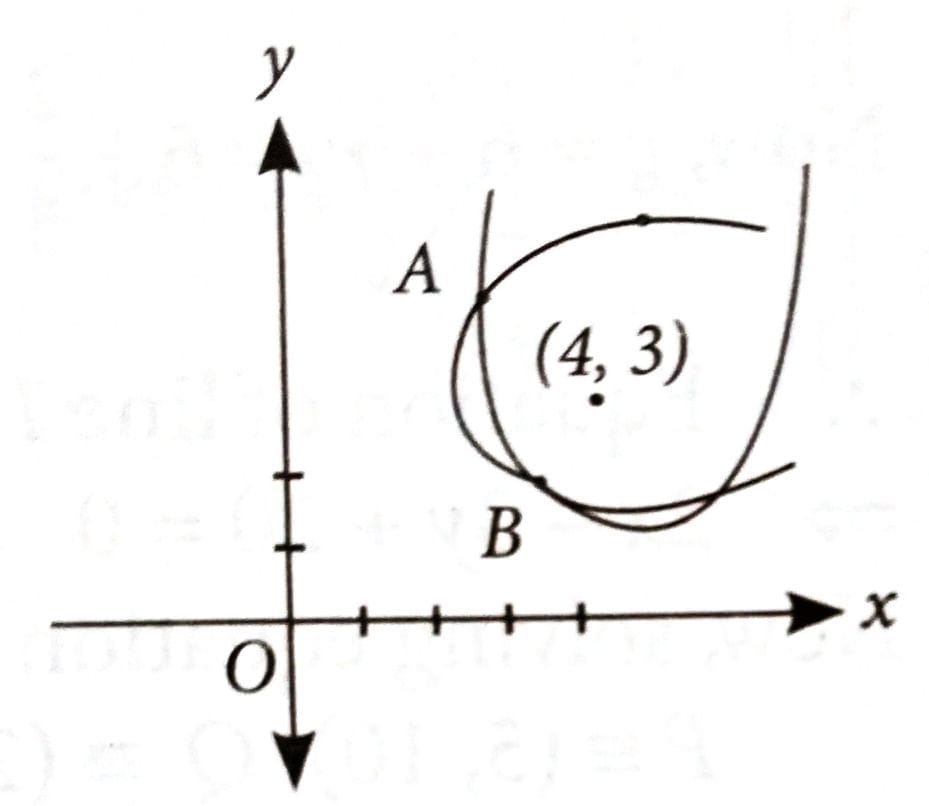
From (i) and (ii), we get x = y
and
.
Q 25
:
The focus of the parabola is the centre of the circle C of radius 5. If the values of , for which C passes through the point of intersection of the lines 3x – y = 0 and x + y = 4, are and , then is equal to __________. [2025]
(15)
We have,
Focus of parabola = (–3, 0) Center (–3, 0)
Equation of circle is given by
Intersection point of 3x – y = 0 and x + y = 4 is
Circle passes through the point of intersection of two lines 3x – y = 0 and x + y = 4.
Now, = –14 + 29 = 15.
Q 26
:
Let A and B be the two points of intersection of the line y + 5 = 0 and the mirror image of the parabola with respect to the line x + y + 4 = 0. If d denotes the distance between A and B, and denotes the area of SAB, where S is the focus of the parabola , then the value of (a + d) is __________. [2025]
(14)
Image of point (0, 0) w.r.t. to line x + y + 4 = 0
Image of focus (1, 0) w.r.t. to line x + y + 4 = 0
Equation of mirror image of parabola
Put y = –5; we get x = –6 and –2
A = (–6, –5); B = (–2, –5)
Distance between the points, d = AB = 4
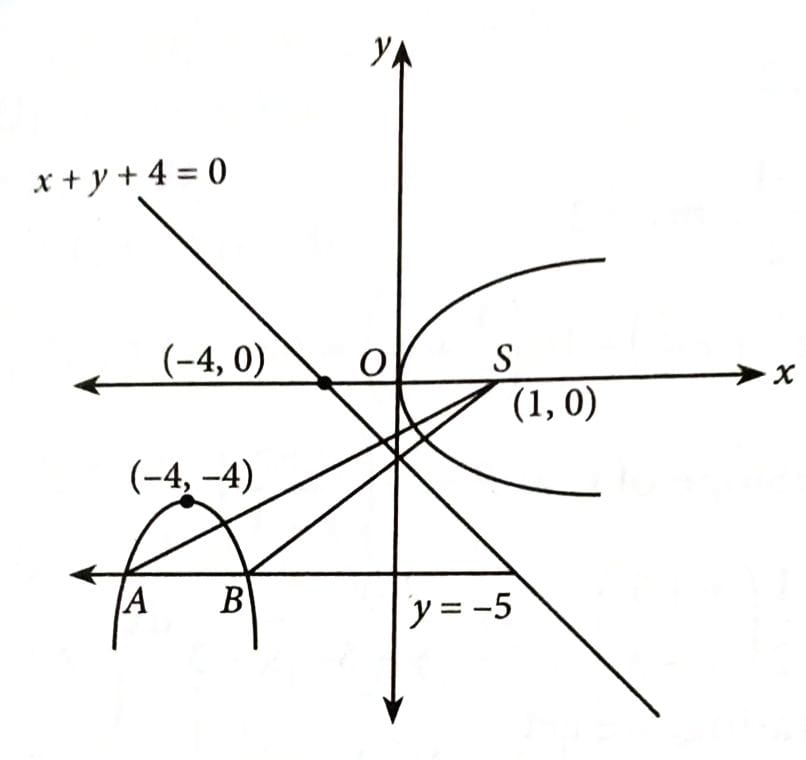
Area of SAB,
So, a + d = 14.
Q 27
:
Let be the parabola and S be its focus. Let PQ be a focal chord of the parabola such that (SP)(SQ) = . Let C be the circle described taking PQ as a diameter. If the equation of a circle C is , then is equal to __________. [2025]
(1328)
Given, equation of parabola is
Focus = S = (3, 0)
Let and are points on parabola
Also,
Now,
( (SP) = PM and (SQ) = QN, where PM and QN are perpendicular distance from directrix)
Case I : When
Points are
Equation of circle is
On comparing with given equation of circle
, we get = 400, = 1728
Case II : When
Point are
Similarly, we get = 400, = 1728
= 1728 – 400 = 1328.
Q 28
:
Let R be the focus of the parabola and the line intersect the parabola at two points P and Q. Let the point G(10,10) be the centroid of the triangle PQR. If = 6, then is [2023]
296
325
346
317
(2)
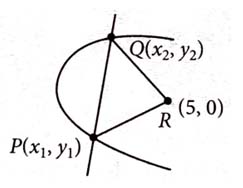
and
Now centroid of is at (10,10)
Q 29
:
Let A(0, 1), B(1, 1) and C(1, 0) be the mid-points of the sides of a triangle with incentre at the point D. If the focus of the parabola passing through D is , where and are rational numbers, then is equal to [2023]
12
6
-
8
(4)
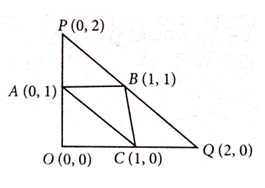
Now, passes through .
So,
The focus of parabola is
So,
Q 30
:
Let PQ be a focal chord of the parabola of length 100, making an acute angle with the positive -axis. Let the ordinate of P be positive and M be the point on the line segment PQ such that PM : MQ = 3 : 1. Then which of the following points does NOT lie on the line passing through M and perpendicular to the line PQ? [2023]
(3, 33)
(- 6, 45)
(6, 29)
(- 3, 43)
(4)

or

