Topic Question Set
Q 11
:
Let the latus rectum of the hyperbola subtend an angle of at the centre of the hyperbola. If is equal to , where and m are co-prime numbers, then is equal to __________. [2024]
(182)
In right triangle OFP, we have
(Given )
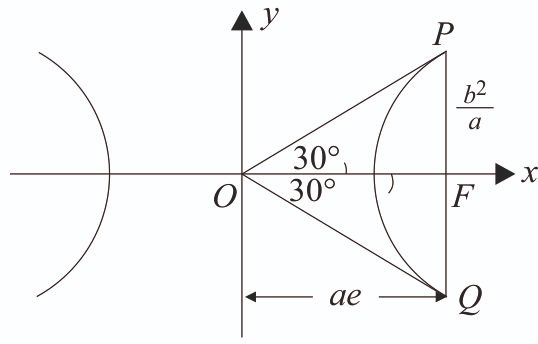
Squaring both sides, we get
... (i)
and ... (ii)
Comparing equation (i) and (ii), we get
According to given condition,
On comparing, we get = 3, m = 2 and n = 13
.
Q 12
:
Let the foci and length of the latus rectum of an ellipse , a > b be (5, 0) and , respectively. Then, the square of the eccentricity of the hyperbola equals [2024]
(51)
Here ae = 5 and
Also,
Now, .
Q 13
:
Let one focus of the hyperbola be at and the corresponding directrix be . If e and respectively are the eccentricity and the length of the latus rectum of H, then is equal to : [2025]
16
15
12
14
(1)
We have,
Now,
and
Q 14
:
Let the sum of the focal distances of the point P(4, 3) on the hyperbola be . If for H, the length of the latus rectum is and the product of the focal distances of the point P is m, then is equal to : [2025]
187
184
185
186
(3)
Given, hyperbola
Sum of focal distance of P(4, 3) =
... (i)
... (ii)
Using (i) and (ii), we get
Now, length of latus rectum,
Also,
.
Q 15
:
Let and be the eccentricities of the ellipse and the hyperbola , respectively. If b < 5 and , then the eccentricity of the ellipse having its axes along the coordinate axes and passing through all four foci (two of the ellipse and two of the hyperbola) is : [2025]
(3)
We have,
(Given)
We get,
Here,
Foci :
The ellipse passing through all four foci is
Now, the eccentricity is given by .
Q 16
:
Let the foci of a hyperbola be (1, 14) and (1, –12). If it passes through the point (1, 6) then the length of its latus-rectum is : [2025]
(4)
Distance between foci
Mid-point of foci
Equation of hyperbola is
Hyperbola passes through (1, 6)
Now,
Length of latus rectum
Q 17
:
Let , a > b and . Let the distane between the foci of E and the foci of H be . If a – A = 2, and the ratio of the eccentricities of E and H is , then the sum of the lengths of their latus rectums is equal to: [2025]
9
7
10
8
(4)
We have, , whose foci are (ae, 0) and , whose foci are (Ae', 0).
Given,
Now, a – A = 2 2A = 1 [a = 3A]
Also,
Sum of latus rectum .
Q 18
:
If A and B are the points of intersection of the circle and the hyperbola and a point P moves on the line 2x – 3y + 4 = 0, then the centroid of PAB lies on the line : [2025]
x + 9y = 36
9x – 9y = 32
4x – 9y = 12
6x – 9y = 20
(4)
We have, ... (i)
and ... (ii)
Solving (i) and (ii), we get
From (i),
and are the points of intersection of circle and hyperbola.
Let be the point moves on the line 2x – 3y + 4 = 0 such that
... (iii)
Centroid of PAB is given by
From (iii), 2(3h –12) – 3(3k) + 4 = 0
i.e., 6x – 9y = 20.
Q 19
:
Let the product of focal distances of the point on the hyperbola be 32. Let the length of the conjugate axis of H be p and the length of its latus rectum be q. Then is equal to __________. [2025]
(120)
We have,
Now, ... (i)
where
ALso,
Now, lies on H
... (ii)
Now,
... (iii)
From equation (ii) and (iii)
Now, .
Q 20
:
If the equation of the hyperbola with foci (4, 2) and (8, 2) is , then is equal to __________. [2025]
(141)
Equation of hyperbola is
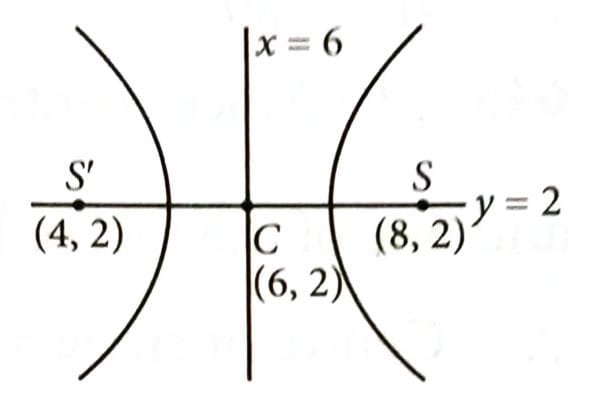
On comparing with , we get and , and

