Q 1 :    

A string is wrapped around the rim of a wheel of moment of inertia $0.40$ $k{m}^2$ and radius 10 cm. The wheel is free to rotate about its axis. Initially the wheel is at rest. The string is now pulled by a force of 40 N. The angular velocity of the wheel after 10 s is $x$ rad/s, where $x$ is _______ .            [2024]

Q 2 :    

A circular disk of radius R meter and mass M kg is rotating around the axis perpendicular to the disk. An external torque is applied to the disk such that $\theta \left(t\right)=5t^2–8t$, where $\theta \left(t\right)$ is the angular position of the rotating disc as a function of time t. How much power is delivered by the applied torque, when t = 2 s?          [2025]

• $60M{R}^2$

   

• $72M{R}^2$

   

• $108M{R}^2$

   

• $8M{R}^2$

   

Q 3 :    

 

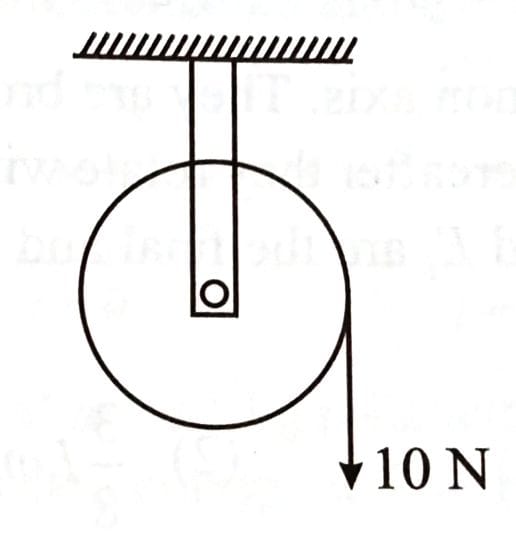
A wheel of radius 0.2 m rotates freely about its center when a string that is wrapped over its rim is pulled by force of 10 N as shown in figure. The established torque produces an angular acceleration of 2 $\mathrm{rad}/{\mathrm{s}}^2$. Moment of inertia of the wheel is _____ ${\mathrm{kgm}}^2$. (Acceleration due to gravity = 10 $\mathrm{m}/{\mathrm{s}}^2$)          [2025]

Q 4 :    

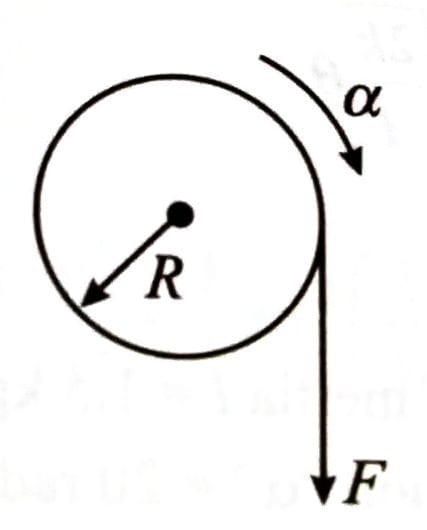
A thin solid disk of 1 kg is rotating along its diameter axis at the speed of 1800 rpm. By applying an external torque of 25 $\pi$Nm for 40 s, the speed increases to 2100 rpm. The diameter of the disk is __________ m.          [2025]