Ans.

(3)

Given the A (a, b), B(3, 4) and C(–6, –8) respectively the centroid, circumcentre and orthocentre of a triangle.

We know that centroid divides circumcentre and orthocentre internally in the ratio 1 : 2

$\therefore a = \frac{–6 + 6}{2}, b = \frac{–8 + 8}{3}$

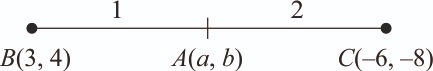
$\Rightarrow$   a = 0, b = 0

Therefore, the coordinates of P are (3, 5).

Also, $l$ : 2x + 3y – 4 = 0 (Given)          ... (i)

Equation of the line passing through P(3, 5) and parallel to the line x – 2y – 1 = 0 is

$y – 5 = \frac{1}{2} (x – 3)$

$\Rightarrow 2y – 10 = x – 3$

$\Rightarrow x – 2y + 7 = 0$          ... (ii)

Solving equation (i) and (ii), we get

$x = \frac{–13}{7}, y = \frac{18}{7}$

$\therefore$   Distance between (3, 5) and $(\frac{–13}{7}, \frac{18}{7})$ is

$\sqrt{{(3 + \frac{13}{7})}^2 + {(5 – \frac{18}{7})}^2} = \sqrt{\frac{1156}{49} + \frac{289}{49}} \sqrt{\frac{1445}{49}} = \frac{17\sqrt{5}}{7}$