Solution
Q.
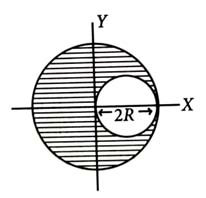
A sphere of radius is cut from a larger solid sphere of radius as shown in the figure. The ratio of the moment of inertia of the smaller sphere to that of the rest part of the sphere about the Y-axis is [2025]