There are two inclined surfaces of equal length (L) and same angle of inclination with the horizontal. One of them is rough and the other is perfectly smooth. A given body takes 2 times as much time to slide down on rough surface than on the smooth surface. The coefficient of kinetic friction () between the object and the rough surface is close to [2025]
0.5
0.75
0.25
0.40
(2)
Given: Angle of inclination,
Length of both inclined surfaces is equal.
For smooth surface, initial velocity is zero, i.e., the distance is given by
Acceleration of smooth plane is
Using , we get
or
For rough surface :
Using , we get
or
As
Squaring on both sides, we get
A horizontal force 10 N is applied to a block A as shown in figure. The mass of blocks A and B are 2 kg and 3 kg, respectively. The blocks slide over a frictionless surface. The force exerted by block A on block B is [2024]
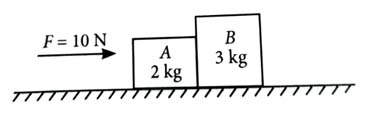
zero
4 N
6 N
10 N
(3)
Common acceleration of the system,
Let R be the contact force between 2 kg and 3 kg blocks.
The free body diagram of 2 kg block is shown in the figure.
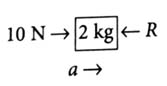
The equation of motion is,
So, the force exerted by block A on B = 6 N
Calculate the maximum acceleration of a moving car so that a body lying on the floor of the car remains stationary. The coefficient of static friction between the body and the floor is 0.15 () [2023]
(1)
Let be the coefficient of friction between the car and the road.
As, retarding force = force of friction
Putting the given values, we get
Which one of the following statements is incorrect? [2018]
Rolling friction is smaller than sliding friction.
Limiting value of static friction is directly proportional to normal reaction.
Frictional force opposes the relative motion.
Coefficient of sliding friction has dimensions of length.
(4)
Coefficient of sliding friction has no dimension.
A plank with a box on it at one end is gradually raised about the other end. As the angle of inclination with the horizontal reaches 30°, the box starts to slip and slides 4.0 m down the plank in 4.0 s. The coefficients of static and kinetic friction between the box and the plank will be, respectively [2015]
0.5 and 0.6
0.4 and 0.3
0.6 and 0.6
0.6 and 0.5
(4)
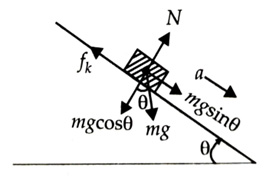
Let and be the coefficients of static and kinetic friction between the box and the plank respectively.
When the angle of inclination reaches , the block just slides,
If is the acceleration produced in the block, then
(where is force of kinetic friction)
As and
...(i)
If is the distance travelled by the block in time , then
But and (given)
Substituting this value of in equation (i), we get
or
A block A of mass rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of the table and from its other end another block B of mass is suspended. The coefficient of kinetic friction between the block and the table is . When the block A is sliding on the table, the tension in the string is [2015]
A system consists of three masses and connected by a string passing over a pulley P. The mass hangs freely and and are on a rough horizontal table (the coefficient of friction = ). The pulley is frictionless and of negligible mass. The downward acceleration of mass is
(Assume ) [2014]
(3)
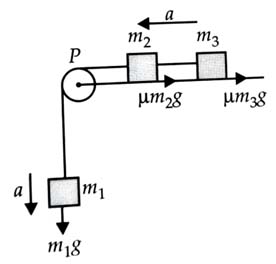
Force of friction on mass
Force of friction on mass
Let be the common acceleration of the system.
Here,