Topic Question Set
Q 61
:
The distance of the line from the point (1, 4, 0) along the line is: [2025]
(4)
Let the parallel line is
and
So, their point of intersection is
and []
So, point of intersection is (2, 6, 3).
So, distance .
Q 62
:
Let the line passing through the points (–1, 2, 1) and parallel to the line intersect the line at the point P. Then the distance of P from the point Q(4, –5, 1) is [2025]
-
-
5
10
(1)
Equation of line passing through (–1, 2, 1) and parallel to is .
Coordinates of P are .
As point P also lies on
Coordinates of point P are
On solving, we get
The point P is (1, 5, 5)
Required distance
Q 63
:
Let in a ABC, the length of the side AC be 6, the vertex B be (1, 2, 3) and the vertices A, C lie on the line . Then the area (in sq. units) of ABC is : [2025]
56
17
42
21
(4)
Let BM be the height of the triangle ABC.
Direction ratios of AC = 3, 2, –2
Coordinates of
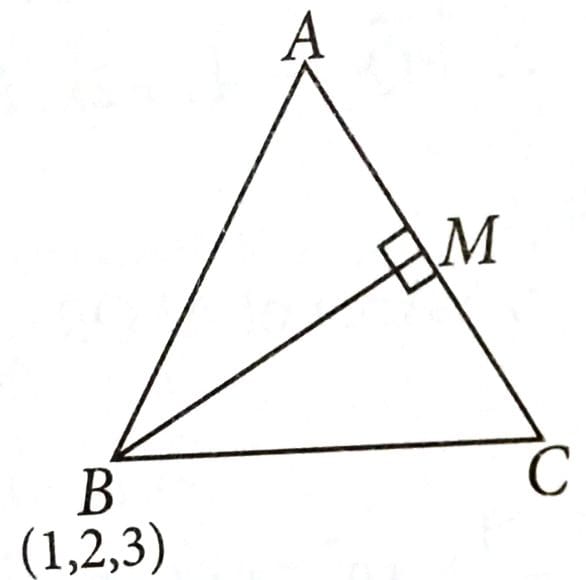
Direction ratios of BM
Coordinates of M = (3, 5, 9)
Area of .
Q 64
:
If the image of the point (4, 4, 3) in the line is , then is equal to [2025]
9
7
12
8
(1)
Let
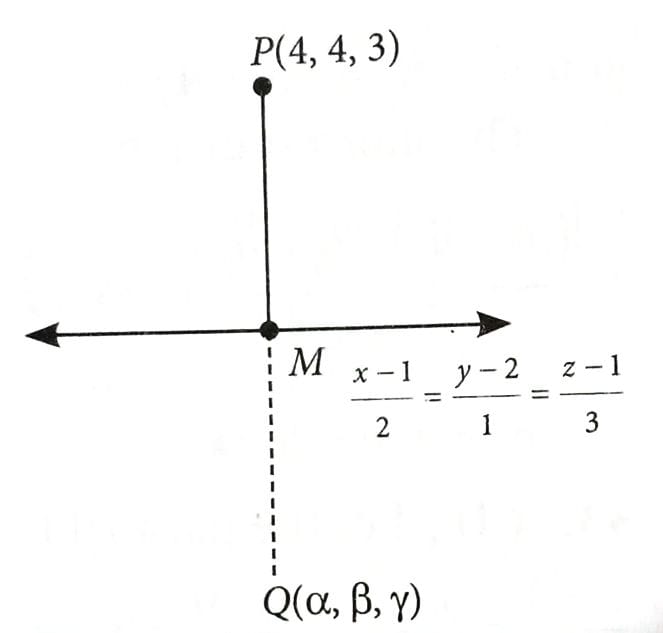
Since, is perpendicular to the given line
The coordinates of point M is (3, 3, 4).
Let Q be the image of the point P. Then, M be the mid-point of PQ.
Q 65
:
The square of the distance of the point from the line in the direction of the vector is : [2025]
66
41
44
54
(1)
Equation of line passing through the point having direction ratios 1, 4 and 7 is given by
It lies on the given line
i.e.,
Square of the distance of the point and
= 1 + 16 + 49 = 66.
Q 66
:
Let A, B, C be three points in xy-plane, whose position vector are given by and respectively with respect to the origin O. If the distance of the point C from the line bisecting the angle between the vectors and is , then the sum of all the possible values of a is : [2025]
1
0
9/2
2
(1)
Equation of line OA is
Equation of line OB is
Equation of angle bisector is
Required sum = 5 + (–4) = 1.
Q 67
:
Let .
Let and be two lines. if the line passes through the point of intersection of and , and is parallel to , then passes through the point: [2025]
(2, 8, 5)
(–1, –1, 1)
(5, 17, 4)
(8, 26, 12)
(4)
We have,
Point of intersection of & is given by
Position vector of point of intersection of and is .
Hence, is given by
For line passes through point (8, 26, 12).
Q 68
:
Let and be two lines.
Let be a line passing through the point and be perpendicular to both and . If intersects , then equals : [2025]
20
25
16
18
(2)
Let D.r.s. of be a, b, c
Now, is to and = a – b + 2c = 0 ... (i)
and –a + 2b + c = 0 ... (ii)
Solving (i) and (ii), we get
Equation of line is
Any point on is
Now,
Any point on is
Now and intersects.
.
Q 69
:
Let ABC be a triangle formed by the lines 7x – 6y + 3 = 0, x + 2y – 31 = 0 and 9x – 2y – 19 = 0. Let the point (h, k) be the image of the centroid of ABC in the line 3x + 6y – 53 = 0. Then is equal to : [2025]
40
36
47
37
(4)
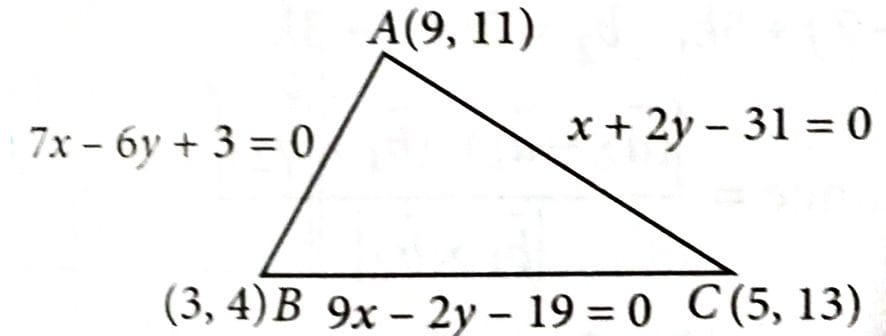
Centroid of
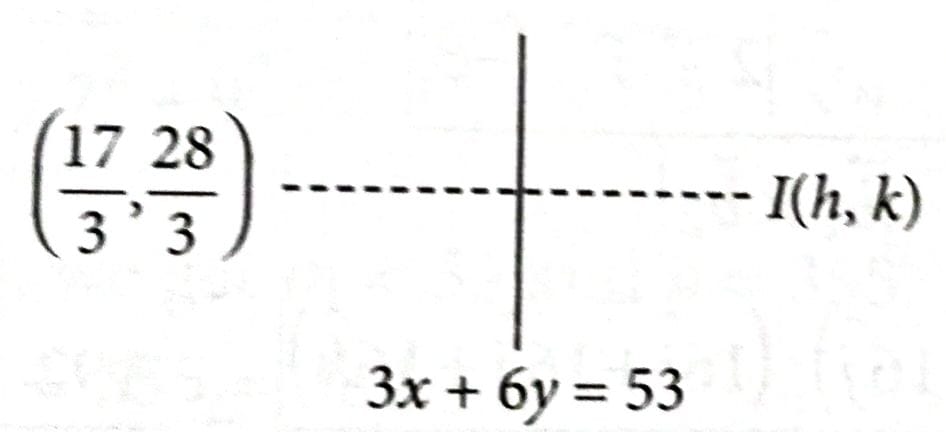
Let image of centroid with respect to line mirror is (h, k).
Solving, we get h = 3 and k = 4
.
Q 70
:
Let P be the foot of the perpendicular from the point (1, 2, 2) on the line . Let the line , intersect the line L at Q. Then is equal to : [2025]
25
19
27
29
(3)
We have,
Now,
Now, line L intersect the other line at Q, i.e.,
So,
Hence, .

