(3)

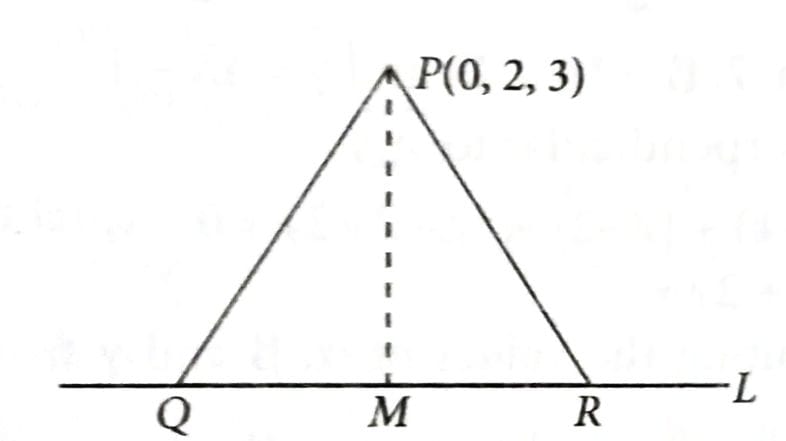
We have, equation of line L is

$\frac{x+3}{5}=\frac{y–1}{2}=\frac{z+4}{3}=\lambda \left(\mathrm{say}\right)$

$\therefore$   Coordinates of $M(5\lambda –3,2\lambda +1,3\lambda –4)$

Dr's of PM are $<5\lambda –3,2\lambda –1,3\lambda –7>$

Dr's of line L are < 5, 2, 3 >

As PM $\perp$ L, so, $(5\lambda –3)5+(2\lambda –1)2+(3\lambda –7)3=0$

$\Rightarrow \lambda =1$

$\therefore$   Coordinates of M is (2, 3, –1)

Now, $PM=\sqrt{{(2–0)}^2+{(3–2)}^2+{(–1–3)}^2}=\sqrt{4+1+16}=\sqrt{21}$

$\therefore$   Area of $△PQR=\frac{1}{2}\times QR\times PM=\frac{1}{2}\times 5\times \sqrt{21}=\frac{m}{n}$

$\Rightarrow 2m–5\sqrt{21}n=0$.

(1)

We have, $L_1:7\hat{i}+6\hat{j}+2\hat{k}+\lambda (–3\hat{i}+2\hat{j}+4\hat{k})$

$L_2:5\hat{i}+3\hat{j}+4\hat{k}+\mu (2\hat{i}+\hat{j}+3\hat{k})$

Here, ${\overrightarrow{a}}_1=7\hat{i}+6\hat{j}+2\hat{k}, {\overrightarrow{a}}_2=5\hat{i}+3\hat{j}+4\hat{k}$

             ${\overrightarrow{b}}_1=–3\hat{i}+2\hat{j}+4\hat{k} \mathrm{and} {\overrightarrow{b}}_2=2\hat{i}+\hat{j}+3\hat{k}$

Now, ${\overrightarrow{b}}_1\times {\overrightarrow{b}}_2=$$\left|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ –3& 2& 4\\ 2& 1& 3\end{array}\right|$

$=\hat{i}(6–4)–\hat{j}(–9–8)+\hat{k}(–3–4)$

$=2\hat{i}+17\hat{j}–7\hat{k}$

Also, ${\overrightarrow{a}}_2–{\overrightarrow{a}}_1=–2\hat{i}–3\hat{j}+2\hat{k}$

Shortest distance between $L_1$ and $L_2$

$=\frac{\left|\right({\overrightarrow{a}}_2–{\overrightarrow{a}}_1)·({\overrightarrow{b}}_1\times {\overrightarrow{b}}_2\left)\right|}{|{\overrightarrow{b}}_1\times {\overrightarrow{b}}_2|}=\frac{|–4–51–14|}{\sqrt{4+289+49}}$

$=\frac{69}{\sqrt{342}}=\frac{69}{3\sqrt{38}}=\frac{23}{\sqrt{38}}$

(4)

Equation of line AB is given by

          $\frac{x–4}{–1}=\frac{y–7}{–2}=\frac{z–1}{2}=\lambda \left(\mathrm{say}\right)$

Any point on line AB is given by $(–\lambda +4,–2\lambda +7,2\lambda +1)$

Now, mid-point of PQ lies on AB i.e.,

$(\frac{1+\alpha }{2},\frac{\beta }{2},\frac{3+\gamma }{2})$ is a point on AB

$\therefore \frac{1+\alpha }{2}=–\lambda +4, \frac{\beta }{2}=–2\lambda +7$ and $\frac{3+\gamma }{2}=2\lambda +1$

$\Rightarrow \alpha =–2\lambda +7, \beta =14–4\lambda \mathrm{and} \gamma =4\lambda –1$           ... (i)

Now, $\overrightarrow{PQ}$ is perpendicular to $\overrightarrow{AB}$

        $\therefore (\alpha –1)(–1)+\beta (–2)+(\gamma –3)\left(2\right)=0$

$\Rightarrow –\alpha –2\beta +2\gamma =5$

Now, substituting the values of $\alpha$, $\beta$ and $\gamma$ from equation (i) we get

         $–(–2\lambda +7)–2(14–4\lambda )+2(4\lambda –1)=5$

$\Rightarrow 2\lambda –7–28+8\lambda +8\lambda –2=5$

$\Rightarrow 18\lambda =42 \Rightarrow \lambda =\frac{7}{3}$

$\therefore \alpha =7–2\times \frac{7}{3}=\frac{7}{3}, \beta =14–4\times \frac{7}{3}=\frac{14}{3}$

and $\gamma =4\times \frac{7}{3}–1=\frac{25}{3}$

$\therefore \alpha +\beta +\gamma =\frac{7}{3}+\frac{14}{3}+\frac{25}{3}=\frac{46}{3}$.

(3)

$L_1\equiv \frac{x–1}{0}=\frac{y–2}{0}=\frac{z–3}{1}$

               [$\because L_1$ is parallel to z-axis and passing through (1, 2, 3)]

and $L_2\equiv \frac{x–\lambda }{0}=\frac{y–5}{1}=\frac{z–6}{0}$

               [$\because L_2$ is parallel to y-axis and passing through $(\lambda ,5,6)$]

Now, shortest distance between $L_1$ and $L_2$ is given by

         $\frac{\left|\begin{array}{ccc}\lambda –1& 3& 3\\ 0& 0& 1\\ 0& 1& 0\end{array}\right|}{\sqrt{{(–1)}^2+0+0}}$$=$$|\lambda –1|$

$\Rightarrow |\lambda –1|=3 \Rightarrow \lambda =4, –2$

$\Rightarrow {\lambda }_1=4, {\lambda }_2=–2$                                                      [$\because {\lambda }_2<{\lambda }_1$]

Let the foot the perpendicular from point P(4, –2, 7) to the line $L_1$ is $Q(1,2,\mu +3)$.

Direction ratios of the QP are (3, –4, 4 – $\mu$)

$\because$  QP is perpendicular to $L_1$

So, $3\times 0–4\times 0+(4–\mu )\times 1=0 \Rightarrow \mu =4$

The coordinates of point Q are (1, 2, 7).

$\therefore P{Q}^2=9+16+0 \Rightarrow P{Q}^2=25$

(3)

$L_1=\frac{x–1}{2}=\frac{y–2}{3}=\frac{z–3}{4}=t \left(\mathrm{say}\right)$

$L_2=\frac{x–6}{1}=\frac{y}{1}=\frac{z–4}{–1}=\mu \left(\mathrm{say}\right)$

A(2t + 1, 3t + 2, 4t + 3) is any point on $L_1$.

And $B(\mu +6,\mu ,4–\mu )$ is any point on $L_2$.

$\therefore$   D.R. of PA = 2t – 3, 3t + 1, 4t + 3 and D.R. of $PB=\mu +2,\mu –1,4–\mu$, where the coordinate of P is (4, 1, 0).

         $\frac{2t–3}{\mu +2}=\frac{3t+1}{\mu –1}=\frac{4t+3}{4–\mu }$

               [Direction ratios of PA and PB are proportional]

         $2t\mu –2t–3\mu +3=3t\mu +6t+\mu +2$

$\Rightarrow t\mu +8t+4\mu –1=0$         ... (i)

Also, $12t–3\mu t+4–\mu =4\mu t+3\mu –4t–3$

$\Rightarrow 7\mu t–16t+4\mu –7=0$          ... (ii)

And $8t–2\mu t–12+3\mu =4\mu t+8t+3\mu +6$

$\Rightarrow 6\mu t=–18 \Rightarrow \mu t=–3$

From equation (i), we get

$8t+4\mu =4 \Rightarrow 2t+\mu =1$          ... (iii)

From equation (ii), we get

$–21–16t+4\mu –7=0$

$16t–4\mu =–28 \Rightarrow 4t–\mu =–7$          ... (iv)

From equation (iii) and (iv), we get

$\therefore t=–1, \mu =3$

$\therefore A(–1,–1,–1) \mathrm{and} B(9,3,1)$

Now, $\left|\begin{array}{ccc}1& 0& 1\\ \alpha & \beta & \gamma \\ a& b& c\end{array}\right|$$=$$\left|\begin{array}{ccc}1& 0& 1\\ –1& –1& –1\\ 9& 3& 1\end{array}\right|$

1(–1 + 3) – 0 + 1(–3 + 9) = 8.

(1)

Let $P\equiv (7,10,11)$

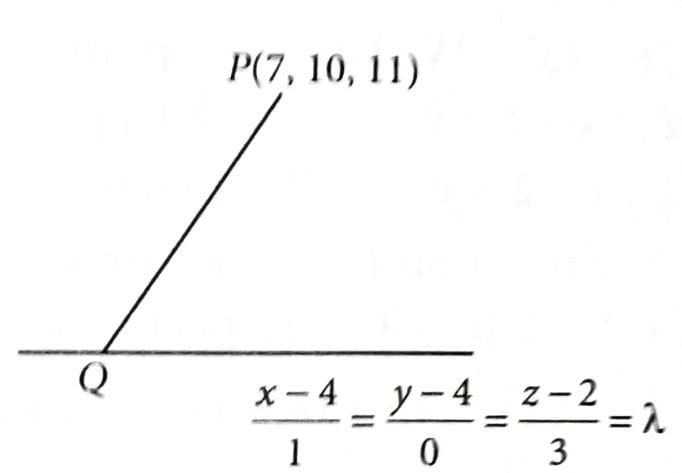
Any point on the line

$L_1:\frac{x–4}{1}=\frac{y–4}{0}=\frac{z–2}{3}=\lambda$

has coordinates

$x=\lambda +4, y=4, z=3\lambda +2$

i.e., $Q(\lambda +4,4,3\lambda +2)$

$\because$   Line PQ is parallel to line

$L_2:\frac{x–9}{2}=\frac{y–3}{3}=\frac{z–17}{6}$

$\Rightarrow \frac{\lambda +4–7}{2}=\frac{4–10}{3}=\frac{3\lambda +2–11}{6} \Rightarrow \lambda =–1$

$\therefore$   Q(3, 4, –1) is the point on the line $L_1$.

Hence, $PQ=\sqrt{16+36+144}=14$ units.

(1)

Given line are $\frac{x–3}{3}=\frac{y–\alpha }{–1}=\frac{z–3}{1}$ and $\frac{x+3}{–3}=\frac{y+7}{2}=\frac{z–\beta }{4}$

Let $A(3,\alpha ,3)$ and $B(–3,–7,\beta )$

$\therefore \overrightarrow{BA}=6\hat{i}+(\alpha +7)\hat{j}+(3–\beta )\hat{k}$

Now, $\overrightarrow{p}\times \overrightarrow{q}=$$\left|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ 3& –1& 1\\ –3& 2& 4\end{array}\right|$$=–6\hat{i}–15\hat{j}+3\hat{k}$

$\therefore$   Shortest distance between lines $=$$\left|\frac{\overrightarrow{BA}·(\overrightarrow{p}\times \overrightarrow{q})}{|\overrightarrow{p}\times \overrightarrow{q}|}\right|$$=3\sqrt{3}$

$\Rightarrow 36+15\alpha +105–9+3\beta =270 \Rightarrow 5\alpha +\beta =46$.

(4)

We have, $L:\frac{x–6}{3}=\frac{y–7}{2}=\frac{z–7}{–2}=\lambda \left(\mathrm{say}\right)$

$\Rightarrow$  Let foot of perpendicular from P(1, 2, 3) on L is 

$Q=(3\lambda +6,2\lambda +7,-2\lambda +7)$

Now, $3(3\lambda +6–1)+2(2\lambda +7–2)–2(-2\lambda +7–3)=0$          [$\because \overrightarrow{PQ}\perp L$]

$\Rightarrow 17\lambda =–17 \Rightarrow \lambda =–1$

Now, distance of A from Q(3, 5, 9) is the foot of perpendicular.

Let any point on line L is $A(3\mu +6,2\mu +7,–2\mu +7)$

Now, distance of A from Q is $2\sqrt{17}$

$\Rightarrow {(3\mu +6–3)}^2+{(2\mu +7–5)}^2+{(–2\mu +7–9)}^2={\left(2\sqrt{17}\right)}^2$

$\Rightarrow 9{\mu }^2+9+18\mu +{4{\mu }^2+4+8\mu +4\mu }^2+4+8\mu =68$

$\Rightarrow 17{\mu }^2+17+34\mu =68 \Rightarrow {\mu }^2+2\mu +1=4$

$\Rightarrow {\mu }^2+2\mu –3=0 \Rightarrow (\mu +3)(\mu –1)=0 \Rightarrow \mu =–3 \mathrm{or} 1$

$\therefore A(–3,1,13) \mathrm{and} B(9,9,5)$ are the points on the line L.

$\therefore \overrightarrow{OA}·\overrightarrow{OB}=–27+9+65=47$.

(2)

We have, $L_1:\frac{x–7}{1}=\frac{y–5}{0}=\frac{z–3}{–1}$ and $L_2:\frac{x–1}{3}=\frac{y+3}{4}=\frac{z+7}{5}$

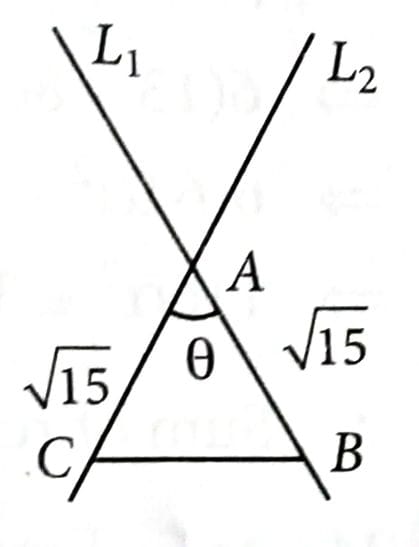
Angle between $L_1$ and $L_2$,

$\cos \theta =$$\left|\frac{3\times 1+4\times 0+5(–1)}{\sqrt{1+0+1}\sqrt{9+16+25}}\right|$$=\frac{1}{5}$

$\Rightarrow \sin \theta =\frac{\sqrt{24}}{5}$

Now, area of $△ABC=\frac{1}{2}ab \sin \theta =\frac{1}{2}{\left(\sqrt{15}\right)}^2\left(\frac{\sqrt{24}}{5}\right)$

So, square of area = $\frac{15\times 15\times 24}{4\times 25}=54$.

(2)

We have lines $\frac{x+1}{3}=\frac{y}{4}=\frac{z}{5}$

$\overrightarrow{r}=(p\hat{i}+2\hat{j}+\hat{k})+\lambda (2\hat{i}+3\hat{j}+4\hat{k})$

where, $\overrightarrow{a}=–\hat{i}+0\hat{j}+0\hat{k}$

$\overrightarrow{b}=p\hat{i}+2\hat{j}+\hat{k} \mathrm{then} \overrightarrow{a}–\overrightarrow{b}=(–1–p)\hat{i}–2\hat{j}–\hat{k}$

$\overrightarrow{p}=3\hat{i}+4\hat{j}+5\hat{k} \mathrm{and} \overrightarrow{q}=2\hat{i}+3\hat{j}+4\hat{k}$

Then, $\overrightarrow{p}\times \overrightarrow{q}=$$\left|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ 3& 4& 5\\ 2& 3& 4\end{array}\right|$

$\Rightarrow \overrightarrow{p}\times \overrightarrow{q}=\hat{i}(16–15)–\hat{j}(12–10)+\hat{k}(9–8)$

                        $=\hat{i}–2\hat{j}+\hat{k}$

Now, shortest distance $=$$\left|\frac{(\overrightarrow{a}–\overrightarrow{b})·(\overrightarrow{p}\times \overrightarrow{q})}{|\overrightarrow{p}\times \overrightarrow{q}|}\right|$

$\Rightarrow \frac{1}{\sqrt{6}}=\frac{\left|\right(–p—1)+4–1|}{\sqrt{1+4+1}} \Rightarrow$$|–p+2|$$=1$

$\Rightarrow$ p = 3 and 1, then a = 1 and b = 3          ($\because$ a < b)

So, length of latus rectum of ellipse $\frac{x^2}{1^2}+\frac{y^2}{3^2}=1$ is $\frac{2a^2}{b}=\frac{2\times 1}{3}=\frac{2}{3}$.