Topic Question Set
Q 61
:
The sum of all local minimum values of the function is [2025]
(4)
Graph of the function f(x)
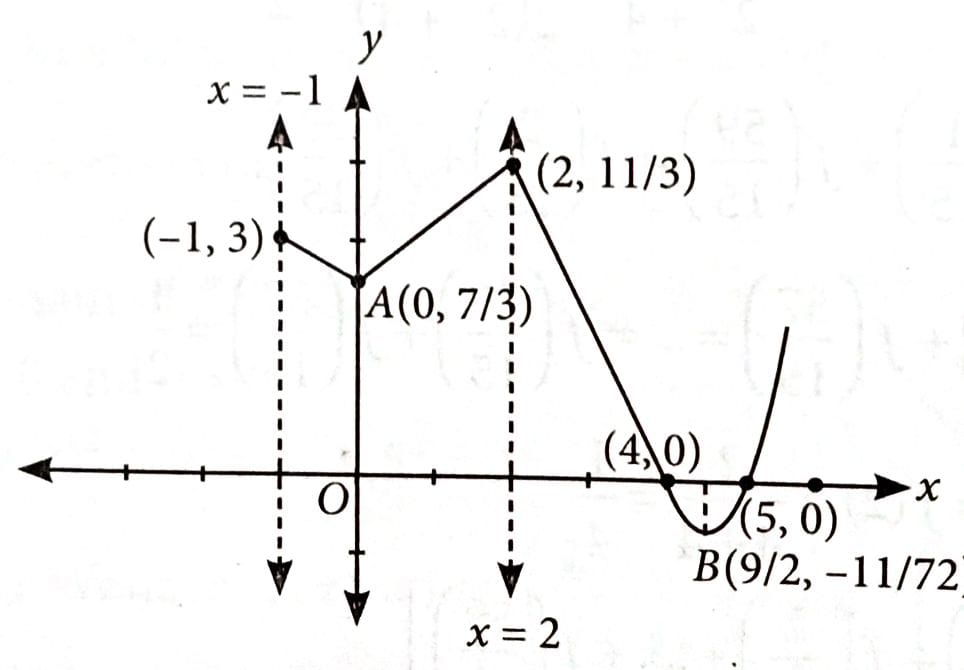
The sum of local minimum values at A and B
.
Q 62
:
If , then is equal to [2025]
-
82
41
-
(1)
We have,
Now,
.
Q 63
:
Let be defined by and be defined by . If both the functions are onto and , then n(S) is equal to: [2025]
36
29
30
31
(3)
As f(x) is onto, hence A is range of f(x).
Now,
for extremum, f(2) = 16 – 60 + 72 + 7 = 35; f(3) = 54 – 135 + 108 + 7 = 34; f(0) = 7; F(1) = 30.
Hence, range [7, 35] = A
Also, for range of g(x), g(x) =
S = {0, 7, 8, ..., 35}
Hence, n(S) = 30
Q 64
:
If the domain of the function is and the domain of the function is , then is equal to : [2025]
195
174
186
179
(3)
Let
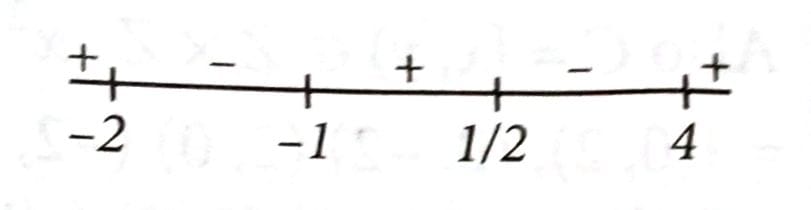
Also, let
,
Now, = 49 + 121 + 16 = 186.

