Topic Question Set
Q 51
:
If the domain of the function is , then is equal to [2025]
18
15
16
17
(1)
For f(x) to be defined we have,
Also,
... (i)
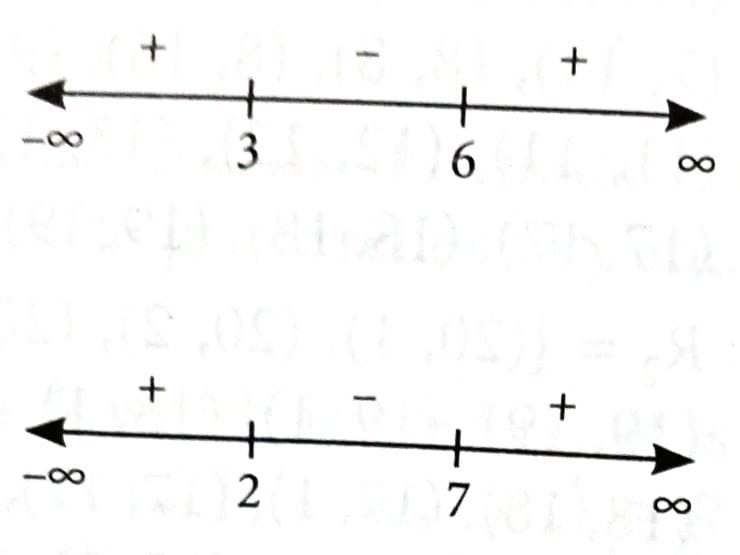
Now,
... (ii)
From equation (i) & (ii), we get
[Given]
Hence, .
Q 52
:
Let f be a function such that . Then f(3) + f(8) is equal to [2025]
13
12
10
11
(4)
We have,
Put x = 3, f(3) + 3f(8) = 12 ... (i)
Put x = 8, f(8) + 3f(3) = 32 ... (ii)
Adding (i) and (ii), we get f(3) + f(8) = 11.
Q 53
:
Let be defined as and . If the range of the function is then is equal to [2025]
56
68
29
2
(1)
Given , ,
also, we have
Now,
i.e.,
Then, .
Q 54
:
Consider the sets , , and . The total number of one-one functions from the set D to the set C is: [2025]
18290
15120
17160
19320
(3)
We Have, ... (i)
... (ii)
... (iii)
Solving (i) and (ii), we get
From (i),
As,
Also,
={(0, 2), (0, –2), (2, 0), (–2, 0), (1, 1), (–1, –1), (–1, 1), (1, –1), (0, 1), (0, –1), (1, 0), (–1, 0), (0, 0)}.
Total number of one-one function from D to C = = 17160.
Q 55
:
If the range of the function , is , then is equal to : [2025]
190
194
188
192
(2)
Case I : If y = 0
x = 5
Case II : if y 0
For real solutions,
From Case I and Case II, we have
.
Q 56
:
Let A = {1, 2, 3, 4} and B = {1, 4, 9, 16}. Then the number of many-one functions f : A B such that is equal to : [2025]
163
139
151
127
(3)
Here, n(A) = 4, n(B) = 4
Total number of functions from A to B = = 256
Number of one-one functions from A to B = = 4! = 24
Number of many-one functions from A to B = 256 – 24 = 232
Number of many-one function for which = 81
Required number of many-one functions = 232 – 81 = 151.
Q 57
:
Let and . Then the domain of fog is [2025]
-
-
-
R
(4)
Given,
Here, []
Also,
The above expression is always positive for any value of x.
.
Q 58
:
Let . Then the value of is equal to [2025]
118
102
92
108
(1)
Q 59
:
The function , defined by is : [2025]
Onto but not one-one
Both one-one and onto
One-one but not onto
Neither one-one nor onto
(3)
Given function is
f(x) is always increasing.
Hence it is one-one.
Since and
Thus, the function f(x) is one-one but not onto.
Q 60
:
Let be a function defined by . If , then the value of is [2025]
675
545
735
715
(1)
Given, ... (i)
Also, ... (ii)
Put x = y = 0 in (ii), we get
f(0) = f(0) + f(0) + 1 – 0 f(0) = –1 ... (iii)
Using (i), f(0) = b = –1
Put y = – x in (ii), we get
Now,
= 675

