Two Dimensional Geometry jee mains questions | JEE Main Two Dimensional Geometry Previous Year Question

Q 1 :
Let PQ be a chord of the parabola $y^{2} = 12 x$ and the midpoint of PQ be at (4, 1). Then, which of the following point lies on the line passing through the points P and Q? [2024]

(2, –9)
$(\frac{3}{2}, - 16)$
$(\frac{1}{2}, - 20)$
(3, –3)

1

2

3

4

(3)

$y^{2} = 12 x$

Chord PQ having mid-point $(x_{1}, y_{1}) \equiv (4, 1)$

Equation of chord PQ

$T = S_{1}$

$y y_{1} - 12 \frac{(x + x_{1})}{2} = y_{1}^{2} - 12 x_{1}$

$\Rightarrow y - 6 (x + 4) = 1 - 12 \times 4$

$\Rightarrow y - 6 x - 24 = - 47 \Rightarrow y - 6 x + 23 = 0$

From the options, point $(\frac{1}{2}, - 20)$ lies on the chord.

Q 2 :
Let C be the circle of minimum area touching the parabola $y = 6 - x^{2}$ and the lines $y = \sqrt{3} | x |$ . Then, which one of the following points lies on the circle C? [2024]

(1, 1)
(2, 4)
(2, 2)
(1, 2)

1

2

3

4

(*)

The given data is inadequate.

Q 3 :
If the shortest distance of the parabola $y^{2} = 4 x$ from the centre of the circle $x^{2} + y^{2} - 4 x - 16 y + 64 = 0$ is d, then $d^{2}$ is equal to : [2024]

16
24
20
36

1

2

3

4

(3)

Circle $x^{2} + y^{2} - 4 x - 16 y + 64 = 0$

Centre $\equiv$ (2, 8), Radius = 2 units

Parabola : $y^{2} = 4 x$

a = 1

Equation of normal at $(t^{2}, 2 t)$ of parabola:

$x t + y = a t^{3} + 2 a t$

$x t + y = t^{3} + 2 t$ ... (i)

[Figure]

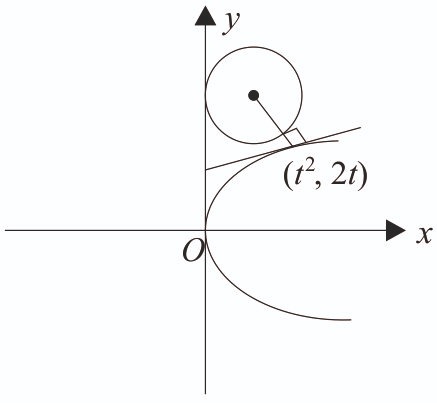
Since, normal passes through centre, then

$2 t + 8 = t^{3} + 2 t$ ... (ii)

$\Rightarrow t^{3} = 8$

$\Rightarrow t^{3} - 8 = 0$

$\Rightarrow (t - 2) (t^{2} + 4 + 2 t) = 0$

$\Rightarrow t = 2 (∵ t \geq 0)$

d = distance between (2, 8) and (4, 4) = $\sqrt{4 + 16} = \sqrt{20}$

$\Rightarrow d^{2} = 20$ .

Q 4 :
Let the length of the focal chord PQ of the parabola $y^{2} = 12 x$ be 15 units. If the distance of PQ from the origin is p, then $10 p^{2}$ is equal to __________. [2024]

0%

(72)

[Figure]

$P Q = 15 \Rightarrow (3 {(t^{2} - \frac{1}{t^{2}}))}^{2} + (6 {(t + \frac{1}{t}))}^{2} = 225$

$\Rightarrow 9 {(t^{2} - \frac{1}{t^{2}})}^{2} + 36 {(t + \frac{1}{t})}^{2} = 225$

$\Rightarrow {(t + \frac{1}{t})}^{2} [{(t - \frac{1}{t})}^{2} + 4] = 25$

$\Rightarrow {(t + \frac{1}{t})}^{2} {(t + \frac{1}{t})}^{2} = 25 \Rightarrow {(t + \frac{1}{t})}^{4} = 25$

$\Rightarrow t + \frac{1}{t} = \pm \sqrt{5} \Rightarrow (t - \frac{1}{t}) = \pm 1$

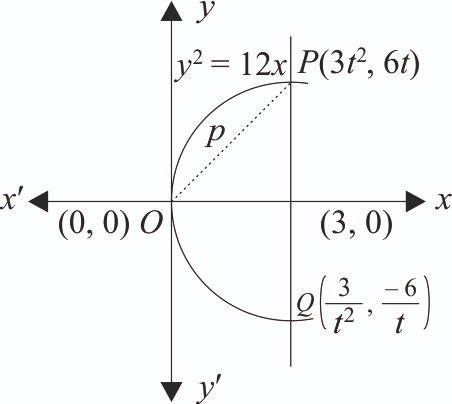
$\Rightarrow$ Equation of PQ : $(y - 6 t) = (\frac{2 t}{t^{2} - 1}) (x - 3 t^{2})$

$\Rightarrow$ Distance from y – 6t = mx – $3 m t^{2}$ , where $m = \frac{2 t}{t^{2} - 1}$

$\Rightarrow p = \frac{| 3 m t^{2} - 6 t |}{\sqrt{1 + m^{2}}} = \frac{| (\frac{6 t}{t^{2} - 1}) |}{\sqrt{5}} = \frac{6}{\sqrt{5}}$

$\Rightarrow 10 p^{2} = \frac{10 \times 36}{5} = 72$ .

Q 5 :
Suppose AB is a focal chord of the parabola $y^{2} = 12 x$ of length $l$ and slope $m < \sqrt{3}$ . If the distance of the chord AB from the origin is d, then $l d^{2}$ is equal to __________. [2024]

0%

(108)

Equation of focal chord

$y - 0 = \tan θ \cdot (x - 3)$

$\Rightarrow \tan θ \cdot x - y - 3 \tan θ = 0$

$∴$ Distance from origin,

$d =$ $| \frac{- 3 \tan θ}{\sqrt{1 + \tan^{2} θ}} |$

$l$ $= 4 \times 3 {cosec}^{2} θ$

$l$ $\cdot d^{2} = \frac{9 \tan^{2} θ}{1 + \tan^{2} θ} \times 12 {cosec}^{2} θ$

$= \frac{108 {cosec}^{2} θ}{1 + \cot^{2} θ} = 108$

Q 6 :
Let a line perpendicular to the line 2x – y = 10 touch the parabola $y^{2} = 4 (x - 9)$ at the point P. The distance of the point P from the centre of the circle $x^{2} + y^{2} - 14 x - 8 y + 56 = 0$ is __________. [2024]

0%

(10)

Let L : 2x – y = 10 and $C : y^{2} = 4 (x - 9)$

Equation of line perpendicular to L is given by

2y + x = k

Now, let us find the point of intersection of 2y + x = k and $y^{2} = 4 (x - 9)$

$i . e ., {(\frac{k - x}{2})}^{2} = 4 (x - 9)$

$\Rightarrow x^{2} - 2 (k + 8) x + (k^{2} + 144) = 0$

As parabola touches the line so this quadratic equation must have at most one real root

$\Rightarrow D = 0$

$\Rightarrow 4 {(k + 8)}^{2} - 4 (k^{2} + 144) = 0$

$\Rightarrow 16 k + 64 - 144 = 0$

$\Rightarrow k = 5$

So, equation becomes $x^{2} - 26 x + 169 = 0$

$\Rightarrow {(x - 13)}^{2} = 0$

$\Rightarrow x = 13$

$\Rightarrow y = \pm 4$

Now, parabola and line 2y + x = 5 meets at P(13, –4)

Now, centre of given circle is (7, 4)

$∴$ Required distance $= \sqrt{{(13 - 7)}^{2} + {(- 4 - 4)}^{2}} = 10$ .

Q 7 :
Let $L_{1}$ , $L_{2}$ be the lines passing through the point P(0, 1) and touching the parabola $9 x^{2} + 12 x + 18 y - 14 = 0$ . Let Q and R be the points on the lines $L_{1}$ and $L_{2}$ such that the $△ P Q R$ is an isosceles triangle with base QR. If the slopes of the lines QR are $m_{1}$ and $m_{2}$ , then $16 (m_{1}^{2} + m_{2}^{2})$ is equal to __________. [2024]

0%

(68)

We have $9 x^{2} + 12 x + 18 y - 14 = 0$

$\Rightarrow 9 x^{2} + 12 x + 4 + 18 y - 18 = 0$

$\Rightarrow {(3 x + 2)}^{2} = - 18 y + 18$

$\Rightarrow {(x + \frac{2}{3})}^{2} = - 2 (y - 1)$

Vertex of parabola is $(\frac{- 2}{3}, 1)$

Now, equation of line passing through (0, 1) is given by y = mx + 1.

Since the line is touching the parabola, so we have

${(x + \frac{2}{3})}^{2} = - 2 m x$

$\Rightarrow {(3 x + 2)}^{2} = - 18 m x$

$\Rightarrow 9 x^{2} + (12 + 18 m) x + 4 = 0$

[Figure]

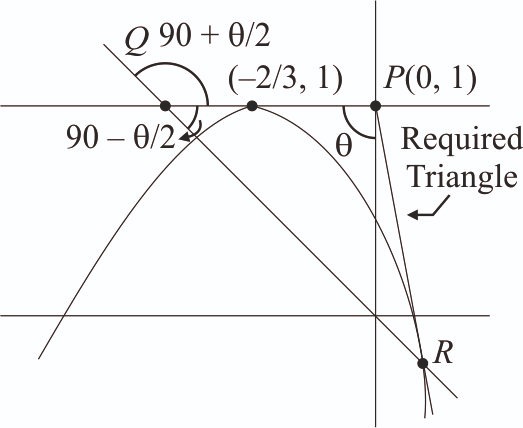
Discriminant of this quadratic equation must be zero.

$\Rightarrow 4 {(6 + 9 m)}^{2} = 4 (36)$

$\Rightarrow 6 + 9 m = 6 or - 6$

$\Rightarrow m = 0, \frac{- 4}{3}$

$∴ \tan θ = \frac{- 4}{3}$

$\Rightarrow \frac{2 \tan θ / 2}{1 - \tan^{2} θ / 2} = \frac{- 4}{3}$

$\Rightarrow - 4 + 4 \tan^{2} θ / 2 - 6 \tan θ / 2 = 0$

$\Rightarrow 2 \tan^{2} θ / 2 - 3 \tan θ / 2 - 2 = 0$

$\Rightarrow (\tan \frac{θ}{2} - 2) (2 \tan \frac{θ}{2} + 1) = 0$

$\Rightarrow \tan \frac{θ}{2} = 2, \frac{- 1}{2}$ ... (i)

Now, in $△ P Q R, ∠ P = θ s o ∠ Q = ∠ R = 90 - \frac{θ}{2}$

$∴ m_{Q R} = \tan (90 + \frac{θ}{2}) = - c o t \frac{θ}{2} = \frac{- 1}{2}, 2$ [Using (i)]

$\Rightarrow m_{1} = \frac{- 1}{2}, m_{2} = 2$

$∴ 16 (m_{1}^{2} + m_{2}^{2}) = 16 (\frac{1}{4} + 4) = 68$ .

Q 8 :
Let a conic C pass through the point (4, –2) and P(x, y), $x \geq 3$ , be any point on C. Let the slope of the line touching the conic C only at a single point P be half the slope of the line joining the points P and (3, –5). If the focal distance of the point (7, 1) on C is d, then 12d equals __________. [2024]

0%

(75)

Slope of C at P $= \frac{1}{2} (\frac{y + 5}{x - 3})$

$\Rightarrow \frac{d y}{d x} = \frac{1}{2} (\frac{y + 5}{x - 3}) \Rightarrow \frac{2 d y}{y + 5} = \frac{1}{x - 3} d x$

On intergrating, we get

2 ln (y + 5) = ln (x – 3) + C

Since, C passes through (4, –2)

$\Rightarrow 2 \ln 3 = C$

$\Rightarrow 2 \ln (y + 5) = \ln (x - 3) + 2 \ln 3$

$\Rightarrow 2 \ln (\frac{y + 5}{3}) = \ln (x - 3) \Rightarrow {(\frac{y + 5}{3})}^{2} = x - 3$

$\Rightarrow {(y + 5)}^{2} = 9 (x - 3)$ , which represent a parabola so, 4a = 9

$\Rightarrow a = \frac{9}{4}$

Focus $= (3 + \frac{9}{4}, - 5) = (\frac{21}{4}, - 5)$

$∴ d = \sqrt{{(\frac{21}{4} - 7)}^{2} + {(- 5 - 1)}^{2}}$

$= \sqrt{{(- \frac{7}{4})}^{2} + {(- 6)}^{2}} = \frac{25}{4}$

$\Rightarrow 12 d = \frac{25}{4} \times 12 = 75$ .

Q 9 :
Let A, B and C be three points on the parabola $y^{2} = 6 x$ and let the line segment AB meet the line L through C parallel to the x-axis at the point D. Let M and N respectively be the feet of the perpendiculars from A and B on L. then ${(\frac{A M \cdot B N}{C D})}^{2}$ is equal to __________. [2024]

0%

(36)

Equation of parabola, $y^{2} = 6 x$

$i . e ., y^{2} = 4 \times \frac{3}{2} x$

Let $A (\frac{3}{2} t_{1}^{2}, 3 t_{1}), B (\frac{3}{2} t_{2}^{2}, 3 t_{2}) and C (\frac{3}{2} t_{3}^{2}, 3 t_{3})$

be points on parabola $y^{2} = 6 x$ .

[Figure]

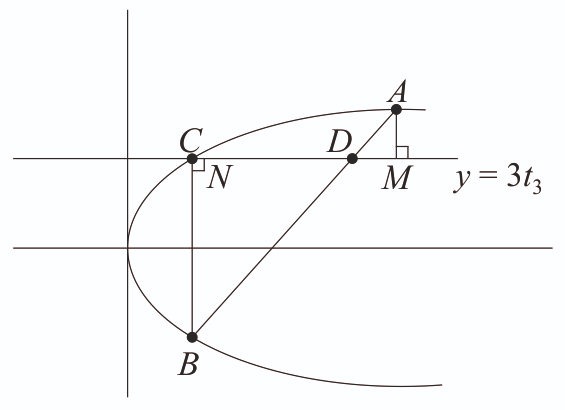
Equation of AB is given by

$\Rightarrow (y - 3 t_{1}) = \frac{3 t_{2} - 3 t_{1}}{\frac{3}{2} (t_{2}^{2} - t_{1}^{2})} (x - \frac{3}{2} t_{1}^{2})$

$\Rightarrow y - 3 t_{1} = \frac{2}{t_{1} + t_{2}} \frac{(2 x - 3 t_{1}^{2})}{2}$

$\Rightarrow (y - 3 t_{1}) (t_{1} + t_{2}) = 2 x - 3 t_{1}^{2}$

$\Rightarrow y (t_{1} + t_{2}) - 3 t_{1}^{2} - 3 t_{1} t_{2} = 2 x - 3 t_{1}^{2}$

$\Rightarrow y (t_{1} + t_{2}) = 2 x + 3 t_{1} t_{2}$

For point D, $y = 3 t_{3}$

$\Rightarrow 2 x = 3 t_{1} t_{3} + 3 t_{2} t_{3} - 3 t_{1} t_{2}$

$\Rightarrow x = \frac{3}{2} (t_{1} t_{3} + t_{2} t_{3} - t_{1} t_{2})$

$| C D | = \frac{3}{2} (t_{1} t_{3} + t_{2} t_{3} - t_{1} t_{2}) - \frac{3}{2} t_{3}^{2}$

$| A M | = | 3 t_{1} - 3 t_{3} |, | B N | = | 3 t_{2} - 3 t_{3} |$

So, ${(\frac{A M \cdot B N}{C D})}^{2} = {(\frac{9 (t_{1} - t_{3}) (t_{2} - t_{3})}{\frac{3}{2} (t_{1} - t_{3}) (t_{3} - t_{2})})}^{2} = {(- 6)}^{2} = 36$ .

Q 10 :
Consider the circle $C : x^{2} + y^{2} = 4$ and the parabola $P : y^{2} = 8 x$ . If the set of all values of $α$ , for which three chords of the circle C on three distinct lines passing through the point $(α, 0)$ are bisected by the parabola P is the interval (p, q), then ${(2 q - p)}^{2}$ is equal to __________. [2024]

0%

(80)

Equation of chord of parabola whose mid-point is $(α, 0)$ is given by $T = S_{1}$

$\Rightarrow y y_{1} - 4 (x + x_{1}) = y_{1}^{2} - 8 x_{1}$

$i . e ., - 4 (x + α) = 0 - 8 α$

$\Rightarrow x = α$

Equation of chord of circle with $A (2 t^{2}, 4 t)$ as mid-point is

$x x_{1} + y y_{1} - 4 = x_{1}^{2} + y_{1}^{2} - 4$

$\Rightarrow 2 t^{2} x + 4 t y = 4 t^{4} + 16 t^{2}$

Also, it passes through $(α, 0)$

$\Rightarrow 2 t^{2} α = 4 t^{4} + 16 t^{2}$

$\Rightarrow 2 α = 4 t^{2} + 16$

$\Rightarrow α = 2 t^{2} + 8 = x_{0} + 8$

Also, we have $x^{2} + y^{2} = 4$ and $y^{2} = 8 x$

$\Rightarrow x^{2} + 8 x - 4 = 0$

$\Rightarrow x_{0} = \frac{- 8 + \sqrt{80}}{2}$

$\Rightarrow p = 8 and q = 4 + 2 \sqrt{5}$

$∴ {(2 q - p)}^{2} = 80$ .

Topic Question Set

Q 1 :
Let PQ be a chord of the parabola $y^{2} = 12 x$ and the midpoint of PQ be at (4, 1). Then, which of the following point lies on the line passing through the points P and Q? [2024]

Q 2 :
Let C be the circle of minimum area touching the parabola $y = 6 - x^{2}$ and the lines $y = \sqrt{3} | x |$ . Then, which one of the following points lies on the circle C? [2024]

Q 3 :
If the shortest distance of the parabola $y^{2} = 4 x$ from the centre of the circle $x^{2} + y^{2} - 4 x - 16 y + 64 = 0$ is d, then $d^{2}$ is equal to : [2024]

Q 4 :
Let the length of the focal chord PQ of the parabola $y^{2} = 12 x$ be 15 units. If the distance of PQ from the origin is p, then $10 p^{2}$ is equal to __________. [2024]

0%

Q 5 :
Suppose AB is a focal chord of the parabola $y^{2} = 12 x$ of length $l$ and slope $m < \sqrt{3}$ . If the distance of the chord AB from the origin is d, then $l d^{2}$ is equal to __________. [2024]

0%

Q 6 :
Let a line perpendicular to the line 2x – y = 10 touch the parabola $y^{2} = 4 (x - 9)$ at the point P. The distance of the point P from the centre of the circle $x^{2} + y^{2} - 14 x - 8 y + 56 = 0$ is __________. [2024]

0%

0%

0%

0%

0%

Want Us to Email you About Special Offers & Updates?

Topic Question Set

Q 1 : Let PQ be a chord of the parabola y2=12x and the midpoint of PQ be at (4, 1). Then, which of the following point lies on the line passing through the points P and Q? [2024]

Q 2 : Let C be the circle of minimum area touching the parabola y=6–x2 and the lines y=3|x|. Then, which one of the following points lies on the circle C? [2024]

Q 3 : If the shortest distance of the parabola y2=4x from the centre of the circle x2+y2–4x–16y+64=0 is d, then d2 is equal to : [2024]

Q 4 : Let the length of the focal chord PQ of the parabola y2=12x be 15 units. If the distance of PQ from the origin is p, then 10p2 is equal to __________. [2024]

0%

Q 5 : Suppose AB is a focal chord of the parabola y2=12x of length l and slope m<3. If the distance of the chord AB from the origin is d, then ld2 is equal to __________. [2024]

0%

Q 6 : Let a line perpendicular to the line 2x – y = 10 touch the parabola y2=4(x–9) at the point P. The distance of the point P from the centre of the circle x2+y2–14x–8y+56=0 is __________. [2024]

0%

0%

0%

Q 9 : Let A, B and C be three points on the parabola y2=6x and let the line segment AB meet the line L through C parallel to the x-axis at the point D. Let M and N respectively be the feet of the perpendiculars from A and B on L. then (AM·BNCD)2 is equal to __________. [2024]

0%

Q 10 : Consider the circle C : x2+y2=4 and the parabola P : y2=8x. If the set of all values of α, for which three chords of the circle C on three distinct lines passing through the point (α, 0) are bisected by the parabola P is the interval (p, q), then (2q–p)2 is equal to __________. [2024]

0%

Want Us to Email you About Special Offers & Updates?

Q 1 :
Let PQ be a chord of the parabola $y^{2} = 12 x$ and the midpoint of PQ be at (4, 1). Then, which of the following point lies on the line passing through the points P and Q? [2024]

Q 2 :
Let C be the circle of minimum area touching the parabola $y = 6 - x^{2}$ and the lines $y = \sqrt{3} | x |$ . Then, which one of the following points lies on the circle C? [2024]

Q 3 :
If the shortest distance of the parabola $y^{2} = 4 x$ from the centre of the circle $x^{2} + y^{2} - 4 x - 16 y + 64 = 0$ is d, then $d^{2}$ is equal to : [2024]

Q 4 :
Let the length of the focal chord PQ of the parabola $y^{2} = 12 x$ be 15 units. If the distance of PQ from the origin is p, then $10 p^{2}$ is equal to __________. [2024]

Q 5 :
Suppose AB is a focal chord of the parabola $y^{2} = 12 x$ of length $l$ and slope $m < \sqrt{3}$ . If the distance of the chord AB from the origin is d, then $l d^{2}$ is equal to __________. [2024]

Q 6 :
Let a line perpendicular to the line 2x – y = 10 touch the parabola $y^{2} = 4 (x - 9)$ at the point P. The distance of the point P from the centre of the circle $x^{2} + y^{2} - 14 x - 8 y + 56 = 0$ is __________. [2024]