jee main chemistry important questions | Chemical Kinetics jee main questions FREE

Q 11 :

${[A]}_{0} / {mol L}^{- 1}$ $t_{1 / 2} / min$

0.100 200

0.025 100

For a given reaction $R \to P$ , $t_{1 / 2}$ is related to ${[A]}_{0}$ as given in the table.
Given: log 2 = 0.30

Which of the following is true?

(A) The order of the reaction is 1/2.

(B) If ${[A]}_{0}$ is 1 M, then $t_{1 / 2}$ is $200 \sqrt{10}$ min.

(C) The order of the reaction changes to 1 if the concentration of reactant changes from 0.100 M to 0.500 M.

(D) $t_{1 / 2}$ is 800 min for ${[A]}_{0}$ = 1.6 M.

Choose the correct answer from the options given below: [2025]

(C) and (D) Only
(A) and (B) Only
(A), (B) and (D) Only
(A) and (C) Only

1

2

3

4

(3)

(A) For $n^{th}$ order reaction, $t_{1 / 2}$ is related to initial concentration $(a_{0})$ as:

$t_{1 / 2} \propto a_{0}^{1 - n}$

$\frac{{(t_{1 / 2})}_{1}}{{(t_{1 / 2})}_{2}} = {(\frac{{(a_{0})}_{1}}{{(a_{0})}_{2}})}^{1 - n}$

$\frac{200}{100} = {(\frac{0.10}{0.025})}^{1 - n}$

$2 = 4^{1 - n}$

$n = \frac{1}{2}$

(B) $\frac{{(t_{1 / 2})}_{for a_{0} = 1 M}}{{(t_{1 / 2})}_{1}} = {(\frac{1}{{(a_{0})}_{1}})}^{1 - n}$

$\frac{{(t_{1 / 2})}_{for a_{0} = 1 M}}{200} = {(\frac{1}{0.1})}^{1 - \frac{1}{2}}$

${(t_{1 / 2})}_{for a_{0} = 1 M} = 200 \sqrt{10} min$

(D) $\frac{{(t_{1 / 2})}_{for a_{0} = 1.6 M}}{{(t_{1 / 2})}_{1}} = {(\frac{1.6}{{(a_{0})}_{1}})}^{1 - n}$

$\frac{{(t_{1 / 2})}_{for a_{0} = 1.6 M}}{200} = {(\frac{1.6}{0.1})}^{1 - \frac{1}{2}}$

${(t_{1 / 2})}_{for a_{0} = 1.6 M} = 800 min$

Q 12 :
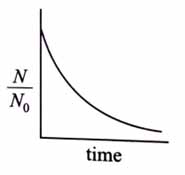
For bacterial growth in a cell culture, growth law is very similar to the law of radioactive decay. Which of the following graphs is most suitable to represent bacterial colony growth?

Where N – Number of Bacteria at any time, $N_{0}$ – Initial number of Bacteria. [2025]

[IMAGE 169]
[IMAGE 170]
[IMAGE 171]
[IMAGE 172]

1

2

3

4

(1)

Initial number of bacteria = $N_{0}$

Number of bacteria at time t = N

Rate of increase of bacteria = $\frac{d N}{d t}$

As bacteria grow by first order:

$\frac{d N}{d t} = k N$

$\frac{d N}{N} = k dt$

Integrate both sides:

$\int_{N_{0}}^{N} \frac{d N}{N} = \int_{0}^{t} k dt$

${[\ln N]}_{N_{0}}^{N} = k {[t]}_{0}^{t}$

$N = N_{0} e^{k t}$

This is exponential growth.

Q 13 :
Drug X becomes ineffective after 50% decomposition. The original concentration of drug in a bottle was 16 mg/mL which becomes 4 mg/mL in 12 months. The expiry time of the drug in months is _______.

Assume that the decomposition of the drug follows first order kinetics. [2025]

6
12
2
3

1

2

3

4

(1)

After every $t_{1 / 2}$ , concentration of reactants in a first order reaction becomes half.

$16 \frac{mg}{mL} \overset{6 months}{\to} 8 \frac{mg}{mL} \overset{6 months}{\to} 4 \frac{mg}{mL}$

So in 6 months, the drug becomes ineffective.

Q 14 :
In a reaction A + B → C, initial concentrations of A and B are related as ${[A]}_{0} = 8 {[B]}_{0}$ . The half-lives of A and B are 10 min and 40 min, respectively. If they start to disappear at the same time, both following first order kinetics, after how much time will the concentration of both the reactants be same? [2025]

60 min
80 min
20 min
40 min

1

2

3

4

(4)

${[A]}_{0}$

$8 M \overset{10 min}{\to} 4 M \overset{10 min}{\to} 2 M \overset{10 min}{\to} 1 M \overset{10 min}{\to} 0.5 M$

${[B]}_{0}$

$1 M \overset{40 min}{\to} 0.5 M$

Q 15 :
Half life of zero order reaction A → product is 1 hour, when initial concentration of reaction is 2.0 mol $L^{- 1}$ . The time required to decrease concentration of A from 0.50 to 0.25 mol $L^{- 1}$ is: [2025]

0.5 hour
4 hour
15 min
60 min

1

2

3

4

(3)

Half-life $(t_{1 / 2})$ of a zero order reaction is related to initial concentration $(a_{0})$ by:

$t_{1 / 2} = \frac{a_{0}}{2 k}$

Thus, rate constant $(k)$ is:
$k = \frac{a_{0}}{2 t_{1 / 2}} = \frac{2 mol/L}{2 \times 1 hour} = \frac{2 mol/L}{2 \times 60 min} = \frac{1}{60} {mol L}^{- 1} {min}^{- 1}$

Concentration at any time $t$ $(a_{t})$ is given by:

$a_{t} = a_{0} - k t,$ $0.25 = 0.5 - (\frac{1}{60}) t, t = 15 min.$

Q 16 :
Reaction A(g) → 2B(g) + C(g) is a first order reaction. It was started with pure A.

t / min Pressure of system at time t / mm Hg

10 160

$\infty$ 240

Which of the following options is incorrect? [2025]

Initial pressure of A is 80 mm Hg.
The reaction never goes to completion.
Rate constant of the reaction is 1.693 $\min^{- 1}$ .
Partial pressure of A after 10 minutes is 40 mm Hg.

1

2

3

4

(3)

$\begin{matrix} A(g) & ⟶ & 2 B(g) & + & C(g) \\ t =0 (pressure) & p ° & 0 & 0 \\ t =10 min & p ° - p & 2 p & p & Total= p ° + 2 p = 160 - (I) \\ t = \infty & 0 & 2 p ° & p ° & Total= 3 p ° = 240 - (II) \end{matrix}$

From equations (I) and (II):

$p ° = 80 mmHg$

$p = 40 mmHg$

Thus, initial pressure of A $(p °) = 80 mmHg$ .

Pressure of A after 10 min

$p ° - p = (80 - 40) mm Hg = 40 mmHg$

First-order reactions never go to completion.

Rate constant:

$k = \frac{2.303}{t} \log \frac{p °}{p ° - p}$

$= \frac{2.303}{10} \log \frac{80}{80 - 40}$

$= \frac{2.303}{10} \log 2$

$= \frac{2.303}{10} \times 0.3 = 0.06909 {min}^{- 1}$

Q 17 :
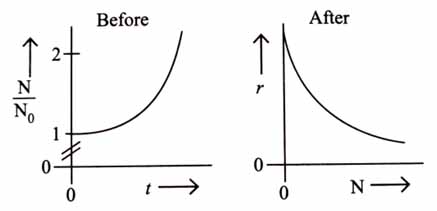
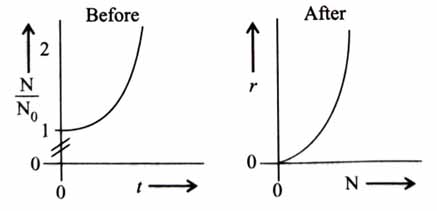
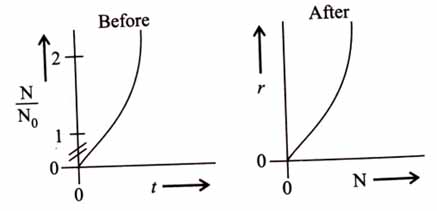
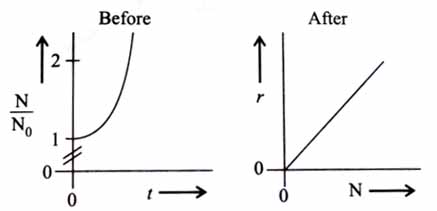
A person’s wound was exposed to some bacteria and then bacterial growth started to happen at the same place. The wound was later treated with some antibacterial medicine and the rate of bacterial decay (r) was found to be proportional with the square of the existing number of bacteria at any instance. Which of the following set of graphs correctly represents the ‘before’ and ‘after’ situation of the application of the medicine?

Given: N = Number of bacteria, t = time, bacterial growth follows first order kinetics. [2025]

[IMAGE 173]
[IMAGE 174]
[IMAGE 175]
[IMAGE 176]

1

2

3

4

(2)

Before applying medicine:

Number of bacteria at any instant t = N

Rate of increase of bacteria = $\frac{d N}{d t}$

As bacterial growth is first order reaction:

$\frac{d N}{d t} = k N$

$\frac{d N}{N} = k dt$

Integrating both sides:

$\int_{N_{0}}^{N} \frac{d N}{N} = \int_{0}^{t} k dt$

${[\ln N]}_{N_{0}}^{N} = k {[t]}_{0}^{t}$

$\ln \frac{N}{N_{0}} = k t$

$\frac{N}{N_{0}} = e^{k t}$

After applying medicine:

Rate of decrease of bacteria $(r) = - \frac{d N}{d t}$
As per given data:

$r = - \frac{d N}{d t} = k {[N]}^{2}$

Q 18 :
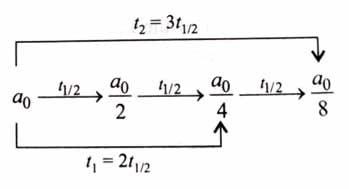
In a first order decomposition reaction, the time taken for the decomposition of reactant to one fourth and one eighth of its initial concentration are $t_{1}$ and $t_{2}$ (s), respectively. The ratio $t_{1} / t_{2}$ will: [2025]

$\frac{4}{3}$
$\frac{3}{2}$
$\frac{3}{4}$
$\frac{2}{3}$

1

2

3

4

(4)

[IMAGE 177]

$\frac{t_{1}}{t_{2}} = \frac{2 t_{1 / 2}}{3 t_{1 / 2}} = \frac{2}{3}$

Q 19 :
For the reaction A → products.

[IMAGE 178]

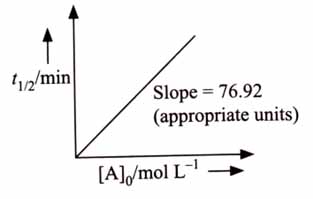
The concentration of A at 10 minutes is ______ $\times 10^{- 3}$ mol $L^{- 1}$ (nearest integer).

The reaction was started with 2.5 mol $L^{- 1}$ of A. [2025]

0%

(2435)

As half-life is directly proportional to initial concentration, the given reaction is a zero-order reaction.

$For zero order reaction: t_{1 / 2} = \frac{a_{0}}{2 k}$

Thus, slope of $t_{1 / 2}$ vs $a_{0}$ is $\frac{1}{2 k}$ .

$As per given in graph, \frac{1}{2 k} = 76.92$

$k = \frac{1}{2 \times 76.92}$

Also, for zero-order reaction, $a_{t} = a_{0} - k t$

$a_{t = 10} = 2.5 - \frac{1}{2 \times 76.92} \times 10 = 2435 \times 10^{- 3} mol/L$

Q 20 :
For the thermal decomposition of $N_{2} O_{5} (g)$ at constant volume, the following table can be formed, for the reaction mentioned below:

$2 N_{2} O_{5} (g) \to 2 N_{2} O_{4} (g) + O_{2} (g)$

Sr. No. Times Total Pressure (atm)

1 0 0.6

2 100 $' x'$

$x$ = _____ $\times 10^{- 3}$ atm (nearest integer)

Given: Rate constant for the reaction is $4.606 \times 10^{- 2} s^{- 1}$ . [2025]

0%

(897)

$\begin{matrix} 2 N_{2} O_{5} (g) & ⟶ & 2 N_{2} O_{4} (g) & + & O_{2} (g) \\ t = 0 & p ° & 0 & 0 \\ t = 100 s & p ° - 2 p & 2 p & p \end{matrix}$

Total pressure at $t = 0$ is $p ° + 0 + 0 = p ° = 0.6$

Total pressure at $t = 100 s$ is $(p ° - 2 p) + 2 p + p = p ° + p = x$

From above two equations, $p = x - 0.6$

For first order reaction, rate constant is given as:

$k = \frac{2.303}{t} \log \frac{P_{N_{2} O_{5}} (t = 0)}{P_{N_{2} O_{5}} (t = t)}$

$4.606 \times 10^{- 2} = \frac{2.303}{100} \log \frac{0.6}{0.6 - 2 (x - 0.6)}$

$4.606 \times 10^{- 2} = \frac{2.303}{100} \log \frac{0.6}{1.8 - 2 x}$

$\log \frac{0.6}{1.8 - 2 x} = 2$

$\frac{0.6}{1.8 - 2 x} = 10^{2} = 100$

$1.8 - 2 x = 0.006$

$x = 0.897 atm = 897 \times 10^{- 3} atm$

Topic Question Set

Q 12 :
For bacterial growth in a cell culture, growth law is very similar to the law of radioactive decay. Which of the following graphs is most suitable to represent bacterial colony growth?

Where N – Number of Bacteria at any time, $N_{0}$ – Initial number of Bacteria. [2025]

Q 13 :
Drug X becomes ineffective after 50% decomposition. The original concentration of drug in a bottle was 16 mg/mL which becomes 4 mg/mL in 12 months. The expiry time of the drug in months is _______.

Assume that the decomposition of the drug follows first order kinetics. [2025]

Q 15 :
Half life of zero order reaction A → product is 1 hour, when initial concentration of reaction is 2.0 mol $L^{- 1}$ . The time required to decrease concentration of A from 0.50 to 0.25 mol $L^{- 1}$ is: [2025]

Q 16 :
Reaction A(g) → 2B(g) + C(g) is a first order reaction. It was started with pure A.

t / min Pressure of system at time t / mm Hg

10 160

$\infty$ 240

Which of the following options is incorrect? [2025]

Q 18 :
In a first order decomposition reaction, the time taken for the decomposition of reactant to one fourth and one eighth of its initial concentration are $t_{1}$ and $t_{2}$ (s), respectively. The ratio $t_{1} / t_{2}$ will: [2025]

Q 19 :
For the reaction A → products.

[IMAGE 178]

The concentration of A at 10 minutes is ______ $\times 10^{- 3}$ mol $L^{- 1}$ (nearest integer).

The reaction was started with 2.5 mol $L^{- 1}$ of A. [2025]

0%

0%

Want Us to Email you About Special Offers & Updates?

${[A]}_{0} / {mol L}^{- 1}$	$t_{1 / 2} / min$
0.100	200
0.025	100

t / min	Pressure of system at time t / mm Hg
10	160
$\infty$	240

Sr. No.	Times	Total Pressure (atm)
1	0	0.6
2	100	$' x'$

Topic Question Set

Q 12 : For bacterial growth in a cell culture, growth law is very similar to the law of radioactive decay. Which of the following graphs is most suitable to represent bacterial colony growth? Where N – Number of Bacteria at any time, N0 – Initial number of Bacteria. [2025]

Q 13 : Drug X becomes ineffective after 50% decomposition. The original concentration of drug in a bottle was 16 mg/mL which becomes 4 mg/mL in 12 months. The expiry time of the drug in months is _______. Assume that the decomposition of the drug follows first order kinetics. [2025]

Q 15 : Half life of zero order reaction A → product is 1 hour, when initial concentration of reaction is 2.0 mol L-1. The time required to decrease concentration of A from 0.50 to 0.25 mol L-1 is: [2025]

Q 16 : Reaction A(g) → 2B(g) + C(g) is a first order reaction. It was started with pure A. t / min Pressure of system at time t / mm Hg 10 160 ∞ 240 Which of the following options is incorrect? [2025]

Q 18 : In a first order decomposition reaction, the time taken for the decomposition of reactant to one fourth and one eighth of its initial concentration are t1 and t2(s), respectively. The ratio t1/t2 will: [2025]

Q 19 : For the reaction A → products. [IMAGE 178] The concentration of A at 10 minutes is ______ ×10-3 mol L-1 (nearest integer). The reaction was started with 2.5 mol L-1 of A. [2025]

0%

0%

Want Us to Email you About Special Offers & Updates?

Q 12 :
For bacterial growth in a cell culture, growth law is very similar to the law of radioactive decay. Which of the following graphs is most suitable to represent bacterial colony growth?

Where N – Number of Bacteria at any time, $N_{0}$ – Initial number of Bacteria. [2025]

Q 13 :
Drug X becomes ineffective after 50% decomposition. The original concentration of drug in a bottle was 16 mg/mL which becomes 4 mg/mL in 12 months. The expiry time of the drug in months is _______.

Assume that the decomposition of the drug follows first order kinetics. [2025]

Q 15 :
Half life of zero order reaction A → product is 1 hour, when initial concentration of reaction is 2.0 mol $L^{- 1}$ . The time required to decrease concentration of A from 0.50 to 0.25 mol $L^{- 1}$ is: [2025]

Q 16 :
Reaction A(g) → 2B(g) + C(g) is a first order reaction. It was started with pure A.

t / min Pressure of system at time t / mm Hg

10 160

$\infty$ 240

Which of the following options is incorrect? [2025]

Q 18 :
In a first order decomposition reaction, the time taken for the decomposition of reactant to one fourth and one eighth of its initial concentration are $t_{1}$ and $t_{2}$ (s), respectively. The ratio $t_{1} / t_{2}$ will: [2025]

Q 19 :
For the reaction A → products.

[IMAGE 178]

The concentration of A at 10 minutes is ______ $\times 10^{- 3}$ mol $L^{- 1}$ (nearest integer).

The reaction was started with 2.5 mol $L^{- 1}$ of A. [2025]