Two Dimensional Geometry jee mains questions | JEE Main Two Dimensional Geometry Previous Year Question

Q 11 :
Let the line $L : \sqrt{2} x + y = α$ pass through the point of the intersection P (in the first quadrant) of the circle $x^{2} + y^{2} = 3$ and the parabola $x^{2} = 2 y$ . Let the line L touch two circles $C_{1}$ and $C_{2}$ of equal radius $2 \sqrt{3}$ . If the centres $Q_{1}$ and $Q_{2}$ of the circle $C_{1}$ and $C_{2}$ lie on the y-axis, then the square of the areas of the triangle $P Q_{1} Q_{2}$ is equal to __________. [2024]

0%

(72)

We have, $L : \sqrt{2} x + y = α$

$x^{2} + y^{2} = 3$ ... (i)

$x^{2} = 2 y$ ... (ii)

Equation (i) and (ii) intersect at $(\sqrt{2}, 1)$ in first quadrant.

$∴ P = (\sqrt{2}, 1) and α = \sqrt{2} \times \sqrt{2} + 1 = 3$

$\Rightarrow α = 3$

Radius of Circle $C_{1}$ and $C_{2} = 2 \sqrt{3}$

We centre $C_{1}$ & $C_{2}$ of two circle are $(0, y_{1})$ and $(0, y_{2})$ respectively.

We know that length of perpendicular from centre to the tangent = Radius of circle

$∴$ $| \frac{\sqrt{2} \times 0 + y - 3}{\sqrt{3}} |$ $= 2 \sqrt{3}$

$\Rightarrow | y - 3 | = 6 \Rightarrow y = 9, - 3$

$∴ y_{1} = - 3, y_{2} = 9$

$∴$ Centre of $C_{1}$ and $C_{2}$ are $Q_{1} (0, - 3)$ and $Q_{2} (0, 9)$ respectively.

$Q_{1} Q_{2} = 12$ units, Height of triangle $= \sqrt{2}$ units

A = Area of triangle $P Q_{1} Q_{2} = \frac{1}{2} \times 12 \times \sqrt{2}$

$[∵ Area of △ P Q_{1} Q_{2} = \frac{1}{2} \times Q_{1} Q_{2} \times height]$

$= 6 \sqrt{2} sq . units$

$\Rightarrow A^{2} = 72$ .

Q 12 :
Let $P (α, β)$ be a point on the parabola $y^{2} = 4 x$ . If P also lies on the chord of the parabola $x^{2} = 8 y$ whose mid point is $(1, \frac{5}{4})$ , then $(α - 28) (β - 8)$ is equal to __________. [2024]

0%

(192)

We $α = t^{2}, β = 2 t$

Now, equation of chord of the parabola $x^{2} = 8 y$ , bisected at $(1, \frac{5}{4})$ is $x \cdot 1 - 2 \times 2 (y + \frac{5}{4}) = 1 - 10$

$\Rightarrow x - 4 y - 5 = - 9 \Rightarrow x - 4 y + 4 = 0$

Now, $(α, β)$ satisfies the above equation

$∴ t^{2} - 8 t + 4 = 0$ ... (i)

Now, $(α - 28) (β - 8) = (t^{2} - 28) (2 t - 8)$

$= (8 t - 4 - 28) (2 t - 8)$ (Using (i))

$= 16 t^{2} - 64 t - 64 t + 256 = 16 (t^{2} - 8 t + 16)$

$= 16 (t^{2} - 8 t + 4 + 12) = 192$ .

Q 13 :
Let the focal chord PQ of the parabola $y^{2} = 4 x$ make an angle of 60° with the positive x-axis, where P lies in the first quadrant. If the circle, whose one diameter is PS, S being the focus of the parabola, touches the y-axis at the point (0, $α$ ), then $5 α^{2}$ is equal to : [2025]

15
25
20
30

1

2

3

4

(1)

Let the coordinate of a point P be $(t^{2}, 2 t)$

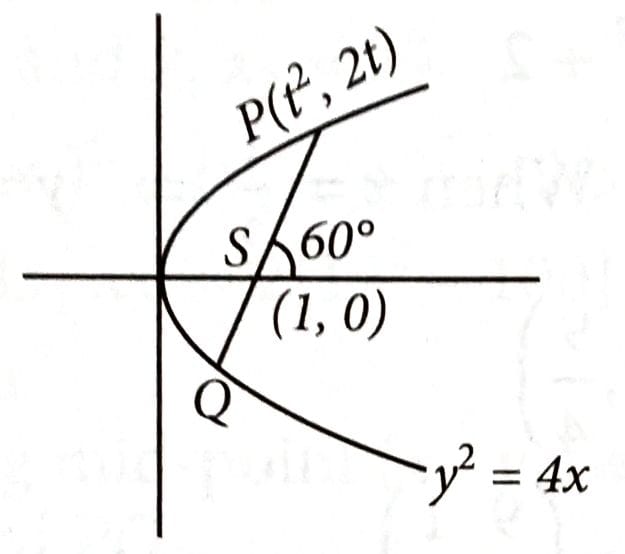
Coordinate of focus S of the parabola is (1, 0).

Now, $\tan 60 ° = \frac{2 t - 0}{t^{2} - 1} = \sqrt{3} \Rightarrow \sqrt{3} t^{2} - 2 t - \sqrt{3} = 0$

$\Rightarrow (\sqrt{3} t + 1) (t - \sqrt{3}) = 0 \Rightarrow t = \sqrt{3}$ { $∵$ P lies in first quadreant}

$∴ P (3, 2 \sqrt{3})$

Equation of circle is $(x - 1) (x - 3) + (y - 0) (y - 2 \sqrt{3}) = 0$

At x = 0, $3 + y^{2} - 2 \sqrt{3} y = 0$

$\Rightarrow {(y - \sqrt{3})}^{2} = 0 \Rightarrow y = \sqrt{3}$

$\Rightarrow y = \sqrt{3} = α$

$∴ 5 α^{2} = 15$ .

Q 14 :
Let the point P of the focal chord PQ of the parabola $y^{2} = 16 x$ be (1, –4). If the focus of the parabola divides the chord PQ in the ratio m : n, gcd (m, n) = 1, then $m^{2} + n^{2}$ is equal to : [2025]

10
17
26
37

1

2

3

4

(2)

End point of the focal chord PQ of the parabola $y^{2} = 4 a x$ is $P (a t^{2}, 2 a t)$

Now, we have parabola $y^{2} = 16 x$

$∴ P (4 t^{2}, 8 t) = (1, - 4)$

$\Rightarrow t = \frac{- 1}{2}$

$∴$ Point Q is given by $(\frac{a}{t^{2}}, - \frac{2 a}{t}) = (16, 16)$

Now, focus of parabola $y^{2} = 16 x$ is (4, 0)

Focus (4, 0) divides P(1, –4) and Q(16, 16) in ratio m : n

$\Rightarrow (4, 0) = (\frac{16 m + n}{m + n}, \frac{16 m - 4 n}{m + n})$

$\Rightarrow 16 m - 4 n = 0 \Rightarrow 4 m = n \Rightarrow \frac{m}{n} = \frac{1}{4}$

$\Rightarrow m = 1, n = 4$ [ $∵$ gcd(m, n) = 1]

$∴ m^{2} + n^{2} = 1 + 16 = 17$ .

Q 15 :
The radius of the smallest circle which touches the parabolas $y = x^{2} + 2$ and $x = y^{2} + 2$ is [2025]

$\frac{7 \sqrt{2}}{2}$
$\frac{7 \sqrt{2}}{16}$
$\frac{7 \sqrt{2}}{4}$
$\frac{7 \sqrt{2}}{8}$

1

2

3

4

(4)

The given parabolas are symmetric about the line y = x.

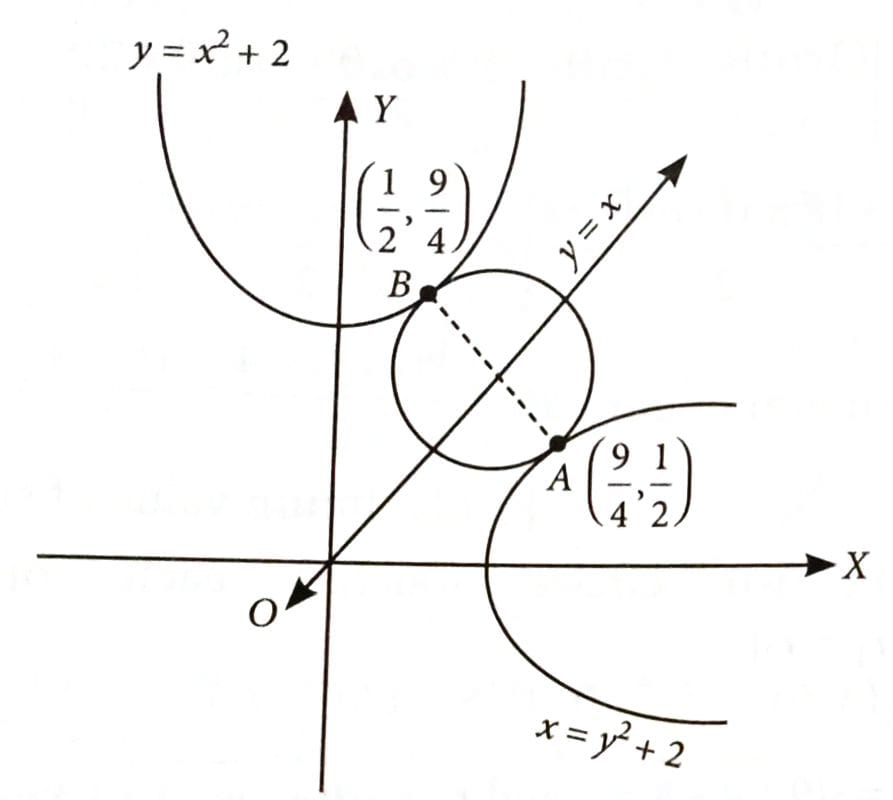
Tangents at A and B must be parallel to line y = x, so slope of the tangents = 1, which is minimum.

${(\frac{d y}{d x})}_{\min A} = 1 = {(\frac{d y}{d x})}_{\min B}$

For point B, $y = x^{2} + 2$

$\Rightarrow \frac{d y}{d x} = 2 x = 1$

When $x = \frac{1}{2} \Rightarrow y = \frac{9}{4}$

$∴ Point B = (\frac{1}{2}, \frac{9}{4})$

Similarly, point $A = (\frac{9}{4}, \frac{1}{2})$

$A B = \sqrt{{(\frac{1}{2} - \frac{9}{4})}^{2} + {(\frac{9}{4} - \frac{1}{2})}^{2}} = \sqrt{\frac{98}{16}} = \frac{7 \sqrt{2}}{4}$

Radius = $\frac{\frac{7 \sqrt{2}}{4}}{2} = \frac{7 \sqrt{2}}{8}$ .

Q 16 :
The axis of a parabola is the line y = x and its vertex and focus are in the first quadrant at distances $\sqrt{2}$ and $2 \sqrt{2}$ units from the origin, respectively. If the point (1, k) lies on the parabola, then a possible value of k is : [2025]

8
4
3
9

1

2

3

4

(4)

For the parabola, axis is y = x

$\Rightarrow$ Directrix is x + y = 0

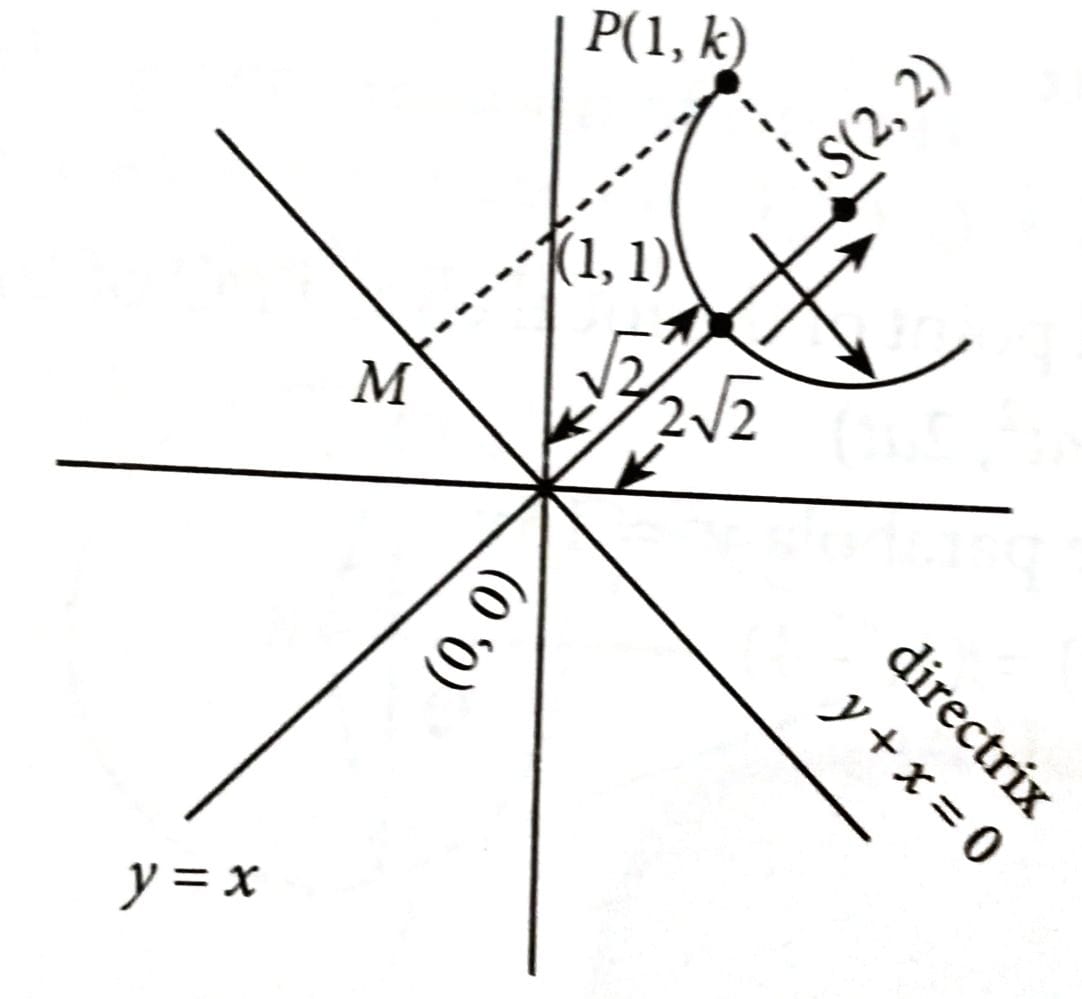
Also, vertex and focus are of $\sqrt{2}$ and $2 \sqrt{2}$ from origin

$\Rightarrow$ Vertex is (1, 1) and focus = (2, 2)

The point P(1, k) lies on parabola.

Using definition of parabola

PS = PM

$\Rightarrow \sqrt{{(1 - 2)}^{2} + {(k - 2)}^{2}} = \frac{1 + k}{\sqrt{2}}$

$\Rightarrow k^{2} - 10 k + 9 = 0$

$\Rightarrow (k - 9) (k - 1) = 0$

$∴$ k = 9 and k = 1.

Q 17 :
Let P be the parabola, whose focus is (–2, 1) and directrix is 2x + y + 2 = 0. Then the sum of the ordinates of the points on P, whose abscissa is –2, is [2025]

$\frac{5}{2}$
$\frac{3}{2}$
$\frac{3}{4}$
$\frac{1}{4}$

1

2

3

4

(2)

Equation of parabola.

${(x + 2)}^{2} + {(y - 1)}^{2} = {(\frac{2 x + y + 2}{\sqrt{5}})}^{2}$

$\Rightarrow 5 [{(x + 2)}^{2} + {(y - 1)}^{2}] = {(2 x + y + 2)}^{2}$ ... (i)

Put x = –2, in equation (i),

$5 {(y - 1)}^{2} = {(y - 2)}^{2}$

$\Rightarrow 5 (y^{2} - 2 y + 1) = y^{2} - 4 y + 4$

$\Rightarrow 4 y^{2} - 6 y + 1 = 0$

$∴$ The sum of ordinates, $y_{1} + y_{2} = \frac{3}{2}$ .

Q 18 :
Let the parabola $y = x^{2} + p x - 3$ , meet the coordinate axes at the points P, Q and R. If the circle C with centre at (–1, –1) passes through the points P, Q and R, then the area of $△$ PQR is : [2025]

7
4
6
5

1

2

3

4

(3)

Given, equation of parabola is $y = x^{2} + p x - 3$ and equation of circle with centre at (–1, –1) is

${(x + 1)}^{2} + {(y + 1)}^{2} = r^{2}$ ... (i)

Let P( $α$ , 0), Q( $β$ , 0) and R(0, –3) are the three points.

Now, circle passes through point R(0, –3)

$\Rightarrow 1 + {(- 2)}^{2} = r^{2} \Rightarrow 5 = r^{2}$

Put y = 0 in equation (i), we get

${(x + 1)}^{2} + 1 = 5$

$\Rightarrow {(x + 1)}^{2} = 4 \Rightarrow x = 1 o r x = - 3$

$\Rightarrow$ Point are P(1, 0) and (–3, 0)

$∴ Area of △ P Q R = \frac{1}{2}$ $| \begin{matrix} 1 & 0 & 1 \\ - 3 & 0 & 1 \\ 0 & - 3 & 1 \end{matrix} |$ $= 6 sq . units$

Q 19 :
Let $P (4, 4 \sqrt{3})$ be a point on the parabola $y^{2} = 4 a x$ and PQ be a focal chord of the parabola. If M and N are the foot of perpendiculars drawn from P and Q respectively on the directrix of the parabola, then the area of the quadrilateral PQMN is equal to : [2025]

$\frac{34 \sqrt{3}}{3}$
$\frac{343 \sqrt{3}}{8}$
$\frac{263 \sqrt{3}}{8}$
$17 \sqrt{3}$

1

2

3

4

(2)

Since, $P (4, 4 \sqrt{3})$ lies on $y^{2} = 4 a x$

$\Rightarrow 48 = 4 a (4) \Rightarrow 4 a = 12$

$\Rightarrow y^{2} = 12 x$ is equation of parabola

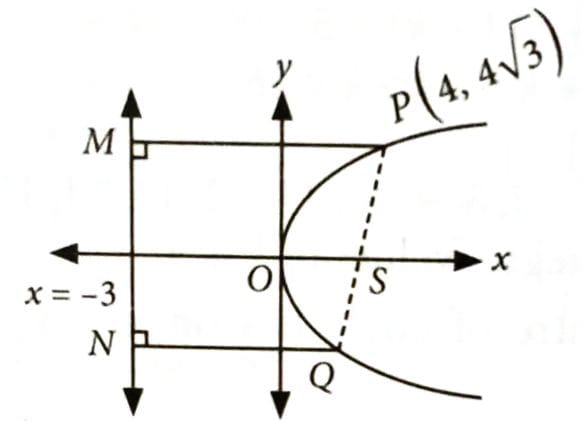
Let $(4, 4 \sqrt{3})$ be $(a t^{2}, 2 a t) \Rightarrow t = \frac{2}{\sqrt{3}}$

As PQ is focal chord

$∴ Q (\frac{a}{t^{2}}, \frac{- 2 a}{t}) = (\frac{9}{4}, - 3 \sqrt{3})$

Area of trapezium PQNM

$= \frac{1}{2} M N (P M + Q N)$

$= \frac{1}{2} M N (P S + Q S)$ [by definition of parabola]

$= \frac{1}{2} \times M N \times P Q$

$= \frac{1}{2} \times 7 \sqrt{3} (\frac{49}{4}) = (343) \frac{\sqrt{3}}{8}$ .

Q 20 :
If the line 3x – 2y + 12 = 0 intersects the parabola $4 y = 3 x^{2}$ at the points A and B, then at the vertex of the parabola, the line segment AB subtends an angle equal to [2025]

$\tan^{- 1} (\frac{11}{9})$
$\tan^{- 1} (\frac{9}{7})$
$\tan^{- 1} (\frac{4}{5})$
$\frac{π}{2} - \tan^{- 1} (\frac{3}{2})$

1

2

3

4

(2)

Given, 3x – 2y + 12 = 0

$\Rightarrow y = \frac{3 x + 12}{2}$

Put value of 'y' in $4 y = 3 x^{2}$ , we get

$\Rightarrow 2 (3 x + 12) = 3 x^{2}$

$\Rightarrow x^{2} - 2 x - 8 = 0 \Rightarrow x = - 2, 4$

$∴$ y = 3, 12

Let A(–2, 3) and B(4, 12)

Since, vertex of parabola is O(0, 0).

$∴ m_{O A} = \frac{- 3}{2}, m_{O B} = \frac{- 12}{- 4} = 3$

$∴ \tan θ =$ $| \frac{m_{O A} - m_{O B}}{1 + m_{O A} \times m_{O B}} |$ $=$ $| \frac{\frac{- 3}{2} - 3}{1 + (\frac{- 3}{2}) \times 3} |$

$\Rightarrow \tan θ = \frac{9}{7} \Rightarrow θ = \tan^{- 1} (\frac{9}{7})$ .

Topic Question Set

0%

Q 12 :
Let $P (α, β)$ be a point on the parabola $y^{2} = 4 x$ . If P also lies on the chord of the parabola $x^{2} = 8 y$ whose mid point is $(1, \frac{5}{4})$ , then $(α - 28) (β - 8)$ is equal to __________. [2024]

0%

Q 13 :
Let the focal chord PQ of the parabola $y^{2} = 4 x$ make an angle of 60° with the positive x-axis, where P lies in the first quadrant. If the circle, whose one diameter is PS, S being the focus of the parabola, touches the y-axis at the point (0, $α$ ), then $5 α^{2}$ is equal to : [2025]

Q 14 :
Let the point P of the focal chord PQ of the parabola $y^{2} = 16 x$ be (1, –4). If the focus of the parabola divides the chord PQ in the ratio m : n, gcd (m, n) = 1, then $m^{2} + n^{2}$ is equal to : [2025]

Q 15 :
The radius of the smallest circle which touches the parabolas $y = x^{2} + 2$ and $x = y^{2} + 2$ is [2025]

Q 16 :
The axis of a parabola is the line y = x and its vertex and focus are in the first quadrant at distances $\sqrt{2}$ and $2 \sqrt{2}$ units from the origin, respectively. If the point (1, k) lies on the parabola, then a possible value of k is : [2025]

Q 17 :
Let P be the parabola, whose focus is (–2, 1) and directrix is 2x + y + 2 = 0. Then the sum of the ordinates of the points on P, whose abscissa is –2, is [2025]

Q 18 :
Let the parabola $y = x^{2} + p x - 3$ , meet the coordinate axes at the points P, Q and R. If the circle C with centre at (–1, –1) passes through the points P, Q and R, then the area of $△$ PQR is : [2025]

Q 19 :
Let $P (4, 4 \sqrt{3})$ be a point on the parabola $y^{2} = 4 a x$ and PQ be a focal chord of the parabola. If M and N are the foot of perpendiculars drawn from P and Q respectively on the directrix of the parabola, then the area of the quadrilateral PQMN is equal to : [2025]

Q 20 :
If the line 3x – 2y + 12 = 0 intersects the parabola $4 y = 3 x^{2}$ at the points A and B, then at the vertex of the parabola, the line segment AB subtends an angle equal to [2025]

Want Us to Email you About Special Offers & Updates?

Topic Question Set

0%

Q 12 : Let P(α, β) be a point on the parabola y2=4x. If P also lies on the chord of the parabola x2=8y whose mid point is (1, 54), then (α–28)(β–8) is equal to __________. [2024]

0%

Q 13 : Let the focal chord PQ of the parabola y2=4x make an angle of 60° with the positive x-axis, where P lies in the first quadrant. If the circle, whose one diameter is PS, S being the focus of the parabola, touches the y-axis at the point (0, α), then 5α2 is equal to : [2025]

Q 14 : Let the point P of the focal chord PQ of the parabola y2=16x be (1, –4). If the focus of the parabola divides the chord PQ in the ratio m : n, gcd (m, n) = 1, then m2+n2 is equal to : [2025]

Q 15 : The radius of the smallest circle which touches the parabolas y=x2+2 and x=y2+2 is [2025]

Q 16 : The axis of a parabola is the line y = x and its vertex and focus are in the first quadrant at distances 2 and 22 units from the origin, respectively. If the point (1, k) lies on the parabola, then a possible value of k is : [2025]

Q 17 : Let P be the parabola, whose focus is (–2, 1) and directrix is 2x + y + 2 = 0. Then the sum of the ordinates of the points on P, whose abscissa is –2, is [2025]

Q 18 : Let the parabola y=x2+px–3, meet the coordinate axes at the points P, Q and R. If the circle C with centre at (–1, –1) passes through the points P, Q and R, then the area of △PQR is : [2025]

Q 19 : Let P(4,43) be a point on the parabola y2=4ax and PQ be a focal chord of the parabola. If M and N are the foot of perpendiculars drawn from P and Q respectively on the directrix of the parabola, then the area of the quadrilateral PQMN is equal to : [2025]

Q 20 : If the line 3x – 2y + 12 = 0 intersects the parabola 4y=3x2 at the points A and B, then at the vertex of the parabola, the line segment AB subtends an angle equal to [2025]

Want Us to Email you About Special Offers & Updates?

Q 12 :
Let $P (α, β)$ be a point on the parabola $y^{2} = 4 x$ . If P also lies on the chord of the parabola $x^{2} = 8 y$ whose mid point is $(1, \frac{5}{4})$ , then $(α - 28) (β - 8)$ is equal to __________. [2024]

Q 14 :
Let the point P of the focal chord PQ of the parabola $y^{2} = 16 x$ be (1, –4). If the focus of the parabola divides the chord PQ in the ratio m : n, gcd (m, n) = 1, then $m^{2} + n^{2}$ is equal to : [2025]

Q 15 :
The radius of the smallest circle which touches the parabolas $y = x^{2} + 2$ and $x = y^{2} + 2$ is [2025]

Q 16 :
The axis of a parabola is the line y = x and its vertex and focus are in the first quadrant at distances $\sqrt{2}$ and $2 \sqrt{2}$ units from the origin, respectively. If the point (1, k) lies on the parabola, then a possible value of k is : [2025]

Q 17 :
Let P be the parabola, whose focus is (–2, 1) and directrix is 2x + y + 2 = 0. Then the sum of the ordinates of the points on P, whose abscissa is –2, is [2025]

Q 18 :
Let the parabola $y = x^{2} + p x - 3$ , meet the coordinate axes at the points P, Q and R. If the circle C with centre at (–1, –1) passes through the points P, Q and R, then the area of $△$ PQR is : [2025]

Q 19 :
Let $P (4, 4 \sqrt{3})$ be a point on the parabola $y^{2} = 4 a x$ and PQ be a focal chord of the parabola. If M and N are the foot of perpendiculars drawn from P and Q respectively on the directrix of the parabola, then the area of the quadrilateral PQMN is equal to : [2025]

Q 20 :
If the line 3x – 2y + 12 = 0 intersects the parabola $4 y = 3 x^{2}$ at the points A and B, then at the vertex of the parabola, the line segment AB subtends an angle equal to [2025]