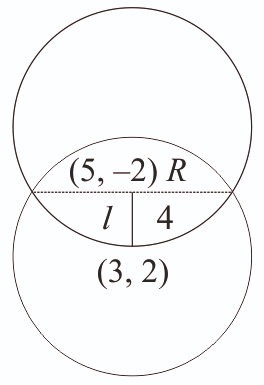
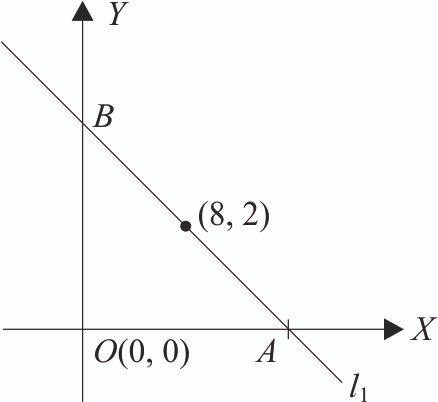
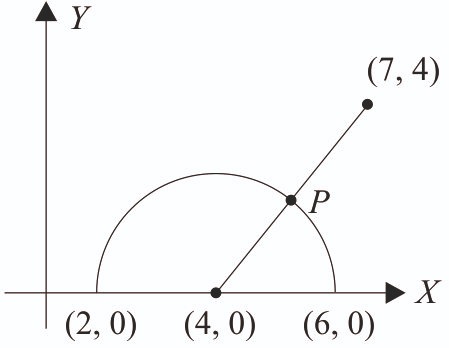
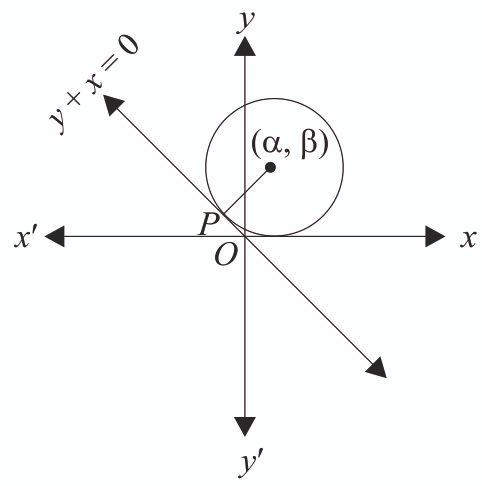
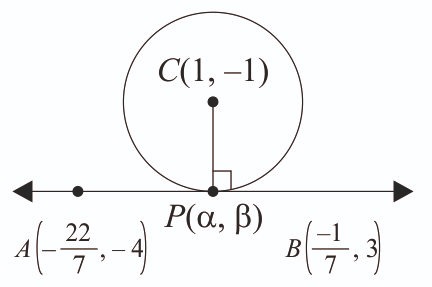
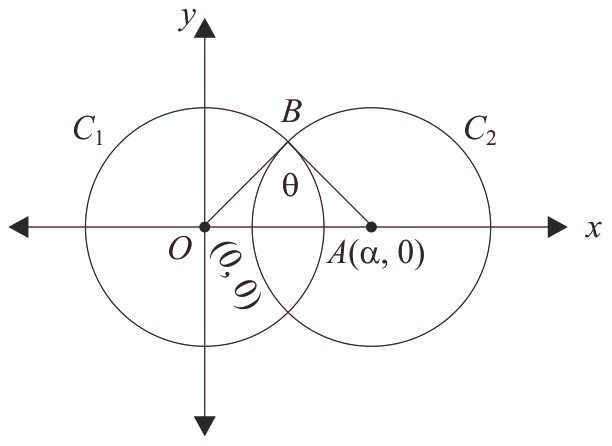
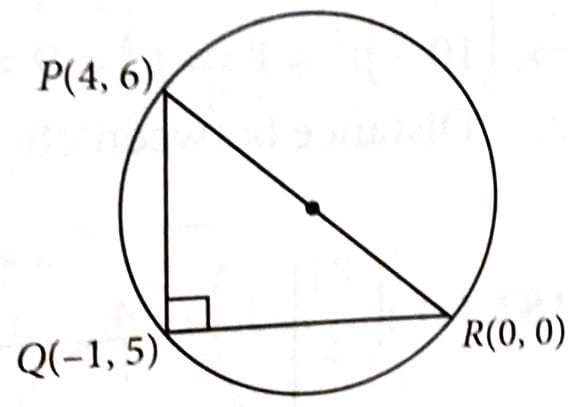
-
 STUDY MATERIALS
STUDY MATERIALS
-
 ONLINE COURSES
ONLINE COURSES
-
 MORE
MORE
Back
- JEE ADVANCE
- JEE MAIN
- NEET
- BITSAT
- CBSE BOARD
- UP BOARD
JEE ADVANCE
- CLASS XI - XII
JEE MAIN
- CLASS XI - XII
NEET
- CLASS XI - XII
BITSAT
- CLASS XI - XII
CBSE BOARD
- CLASS IX
- CLASS X
- CLASS XI
- CLASS XII
- CLASS VI
- CLASS VII
- CLASS VIII
CLASS IX
CLASS X
CLASS XI
CLASS XII
CLASS VI
CLASS VII
CLASS VIII
UP BOARD
- CLASS IX
- CLASS X
- CLASS XI
- CLASS XII
CLASS IX
CLASS X
CLASS XI
Online Courses