Consider a hyperbola H having centre at the origin and foci on the x-axis. Let be the circle touching the hyperbola H and having the centre at the origin. Let be the circle touching the hyperbola H at its vertex and having the centre at one of its foci. If areas (in sq. units) of and are 36 and 4, respectively, then the length (in units) of latus rectum of H is [2024]
(1)
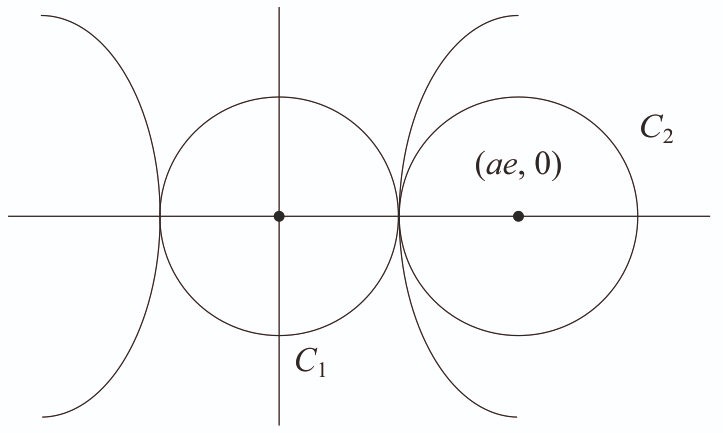
Length of Latus Rectum = units.
Let be the hyperbola, whose eccentricity is and the length of the latus rectum is . Suppose the point (, 6), > 0 lies on H. If is the product of the focal distances of the point (, 6), then is equal to [2024]
169
171
172
170
(2)
and
Now,
Length of latus rectum [Given]
[ a > 0]
Now, P(, 6) lies on
Now, foci of hyperbola = (0, be) = (0, 3)
Let and be focal distancee of (, 6)
Now,
Now, .
Let the foci of a hypebola H coincide with the foci of the ellipse and the eccentriticy of the hyperbola H be the reciprocal of the eccentricity of the ellipse E. If the length of the transverse axis of H is and the length of its conjugate axis is , then is equal to [2024]
237
225
205
242
(2)
Eccentricity of ellipse E i.e.,
So, eccentricity of hyperbola = 2
Now, foci of ellipse = (1 ae, 1) = (1 5, 1)
= (6, 1) and (–4, 1) = Foci of hyperbola
Now, distance between foci =
Also,
Length of transverse axis of H = 2a =
Length of conjugate axis of H = 2b =
Now, .
For 0 < < /2, if the eccentricity of the hyperbola is times eccentricity of the ellipse , then the value of is [2024]
(2)
Given,
... (i)
Also, (Given)
... (ii)
Given, eqn. (i) = eqn. (ii)
Squaring on both sides.
So, .
Let be the eccentricity of the hyperbola and be the eccentricity of the ellipse , a > b, which passes through the foci of the hyperbola. If , then the length of the chord of the ellipse parallel to the x-axis and passing through (0, 2) is [2024]
(2)
Given hyperbola is
= eccentricity of hyperbola =
Foci of hyperbola = (5, 0)
Given
= eccentricity of ellipse
... (i)
The ellipse also passes through the foci of the hyperbola.
From (i),
Thus, the equation of ellipse is ... (ii)
Now, equation of chord of ellipse which passes through (0, 2) and parallel to x-axis is y = 2.
From (ii),
Thus, the end point of chord are .
Length of chord = .
Let P be a point on the hyperbola in the first quadrant such that the area of triangle formed by P and the two foci of H is . Then, the square of the distance of P from the origin is [2024]
20
18
26
22
(4)
We have,
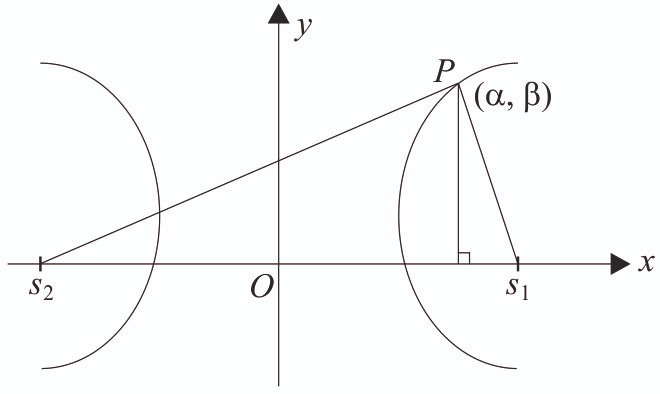
Here,
Area of
Distance of P from origin = .
If the foci of a hyperbola are same as that of the ellipse and the eccentricity of the hyperbola is times the eccentricity of the ellipse, then the smaller focal distance of the point on the hyperbola, is equal to [2024]
(1)
We have,
foci : (0, 5e)
Since, for an ellipes,
Eccentricity of hyperbola =
Focus of hyperbola = (0, 5e) = (0, 4)
Since,
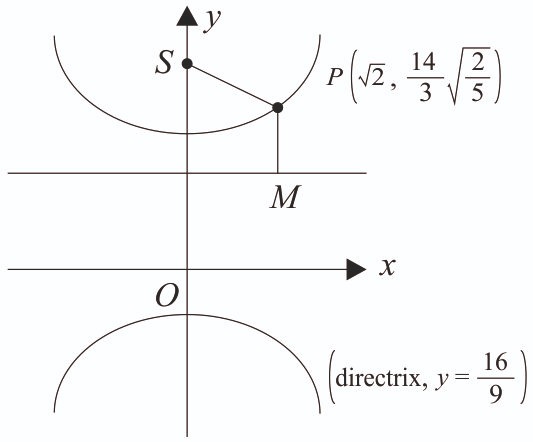
The equation of hyperbola
PS =
.
Let A be a square matrix of order 2 such that |A| = 2 and the sum of its diagonal elements is –3. If the points (x, y) satisfying + xA + y = O lie on a hyperbola, whose transverse axis is parallel to the x-axis, eccentricity is e and the length of the latus rectum is , then is equal to ___________. [2024]
(*)
The given data is inadequate.
The length of the latus rectum and directrices of a hyperbola with eccentricity e are 9 and , respectively. Let the line touch this hyperbola at . If m is the product of the focal distances of the point , then is equal to __________. [2024]
(*)
Equation of tangent to hyperbola is given by
and
... (i)
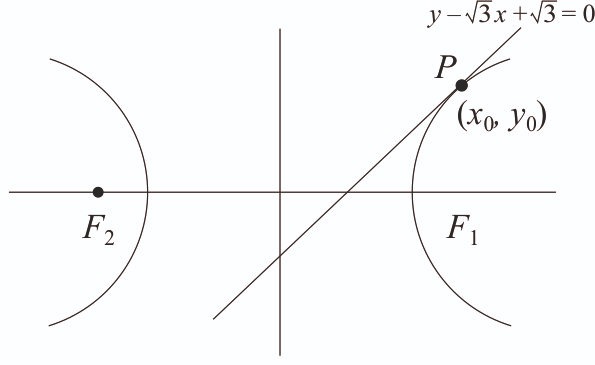
Now, length of latus rectum of hyperbola = 9
... (ii)
From equation (i) and (ii), we get
Equation of hyperbola is
Solving for tangent , we get
So, is the point of contact.
Focus of hyperbola is
Note: Here equation of directrix should be , but in given question it is given which is wrong because eccentricity should be greater than 1, So, this question is bonus.
Let S be the focus of the hyperbola , on the positive x-axis. Let C be the circle with its centre at and passing through the point S. If O is the origin and SAB is a diameter of C, then the square of the area of the triangle OSB is equal to __________. [2024]
(40)
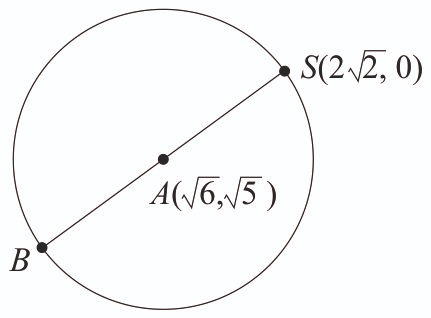
A is mid-point of BS
Area of ,
.