A square is inscribed in the circle . One side of this square is parallel to y = x + 3. If are the vertices of the square, then is equal to [2024]
160
152
156
148
(2)
One side of square is y = x + k
Distance of (5, 3) to the line y = x + k is
So lines are y = x and y = x – 4
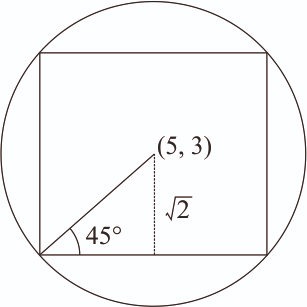
Now, solving these lines with circle
y = x and
x = 3, y = 3 and x = 5, y = 5
and y = x – 4 and
x = 5, y = 1 and x = 7, y = 3
= 9 + 9 + 25 + 25 + 25 + 1 + 49 + 9 = 152.
Let C be a circle with radius units and centre at the origin. Let the line x + y = 2 intersects the circle C at the points P and Q. Let MN be a chord of C of length 2 units and slope –1. Then a distance (in units) between the chord PQ and the chord MN is [2024]
(1)
Distance of centre from chord
Let distance of centre from chord MN = p, then length of chord =
( Given)
Distance between chord PQ and MN = .
Let a circle C of radius 1 and closer to the origin be such that the lines passing through the point (3, 2) and parallel to the coordinate axes touch it. Then the shortest distance of the circle C from the point (5, 5) is: [2024]
4
5
(3)
Centre of circle = (2, 1)
Equation of circle will be
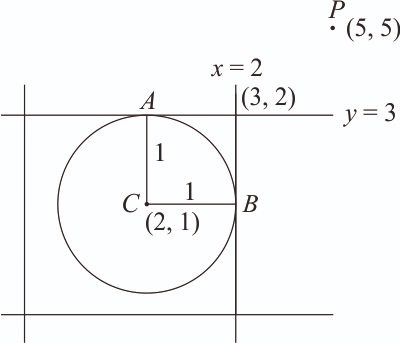
Distance between C(2, 1) and P(5, 5)
=
= 5 units
Also, AC = BC = 1 unit [ Radius = 1]
Shortest distance of circle from P = 5 – 1 = 4 units.
Let the circle and be a circle having centre at (–1, 0) and radius 2. If the line of the common chord of and intersects the y-axis at the point P, then the square of the distance of P from the centre of is: [2024]
2
6
4
1
(1)
We have,
For common chord, we have
Since, common chord intersects y-axis
So, x = 0
y = 2
So, point of intersection of common chord with y-axis is P(0, 2).
Required distance = .
Let ABCD and AEFG be squares of sides 4 and 2 units respectively. the point E is on the line segment AB and the point F is on the diagonal AC. Then the radius r of the circle passing through the point F and touching the line segments BC and CD satisfies : [2024]
r = 1
(2)
Let r be the radius of circle and centre at C(r, r).
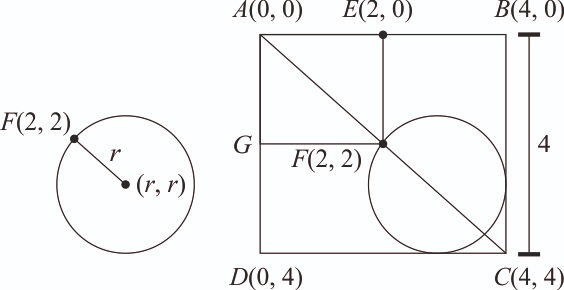
Then,
.
Let the circles and touch each other externally at the point (6, 6). If the point (6, 6) divides the line segment joining the centres of the circles and internally in the ratio 2 : 1, then equals [2024]
110
125
145
130
(4)
are the centres of circle and respectively. Now, A(6, 6) is the given point.
A divides BC in ratio 2 : 1
and
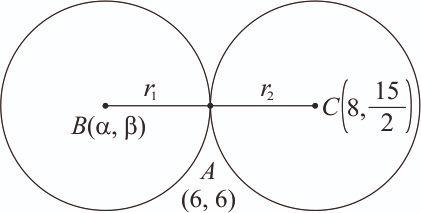
Also,
.
If the image of the point (–4,5) in the line x + 2y = 2 lies on the circle , then r is equal to : [2024]
1
4
3
2
(4)
Image lies on circle
Let a circle passing through (2,0) have its centre at the point (h, k). Let be the point of intersection of the lines 3x + 5y = 1 and . If and , then the equation of the circle is : [2024]
(3)
We have, 3x + 5y = 1 ... (i)
... (ii)
Multiplying (i) by and subtracting it from (ii), we get
Now,
and
Equation of circle is
[ Circle passes through (2, 0)]
Let and be two circles. If the set of all values of so that the circles C and C' intersect at two distinct points, is R – [a, b], then the point (8a + 12, 16b – 20) lies on the curve : [2024]
(2)
We have, ... (i)
and
... (ii)
Radius of C, and radius of C',
When two circles intersect at two points,
then
...(iii)
By (iii), we have
On Squaring both sides, we get
Also, [By (iii)]
On squaring, we get
Thus, Circles C and C' intersect at two distinct points for
(8a + 12, 16b –20) = (–1, 6) which satisfies only .
Let the locus of the midpoints of the chords of the circle drawn from the origin intersect the line x + y = 1 at P and Q. Then, the length of PQ is : [2024]
1
(3)
Let be the mid point of chords.
So, equation of chord of the circle is,
The chord is passing through origin
... (i)
Now, (i) intersects the line x + y = 1
If , then [From (i)]
If y = 1, then
So, and Q = (1, 0)