Three Dimensional Geometry jee mains questions with solutions

Q 71 :

Let a straight line L pass through the point P(2, –1, 3) and be perpendicular to the lines $\frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z - 3}{- 2}$ and $\frac{x - 3}{1} = \frac{y - 2}{3} = \frac{z + 2}{4}$ . If the line L intersects the yz-plane at the point Q, then the distance between the points P and Q is : [2025]

$\sqrt{10}$
2
3
$2 \sqrt{3}$

1

2

3

4

(3)

Vector parallel to line $L =$ $| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & - 2 \\ 1 & 3 & 4 \end{matrix} |$

$= 10 \hat{i} - 10 \hat{j} + 5 \hat{k} = 5 (2 \hat{i} - 2 \hat{j} + \hat{k})$

Equation of line L passing through point P(2, –1, 3) and parallel to vector $(2 \hat{i} - 2 \hat{j} + \hat{k})$ , is

$\frac{x - 2}{2} = \frac{y + 1}{- 2} = \frac{z - 3}{1} = λ$

$∴ x = 2 λ + 2, y = - 2 λ - 1, z = λ + 3$

$∵$ Line L intersects the yz-plane

$∴ 2 λ + 2 = 0 \Rightarrow λ = - 1$

Hence, point Q is (0, 1, 2)

Distance between point P(2, –1, 3) and Q(0, 1, 2)

$= \sqrt{{(0 - 2)}^{2} + {(1 + 1)}^{2} + {(2 - 3)}^{2}} = \sqrt{9} = 3$ .

Q 72 :

Let the area of the triangle formed by the lines x + 2 = y – 1 = z, $\frac{x - 3}{5} = \frac{y}{- 1} = \frac{z - 1}{1}$ and $\frac{x}{- 3} = \frac{y - 3}{3} = \frac{z - 2}{1}$ be A. Then $A^{2}$ is equal to __________. [2025]

0%

(56)

$L_{1} : x + 2 = y - 1 = z = λ (say)$

$L_{2} : \frac{x - 3}{5} = \frac{y}{- 1} = \frac{z - 1}{1} = μ (say)$

$L_{3} : \frac{x}{- 3} = \frac{y - 3}{3} = \frac{z - 2}{1} = δ (say)$

Any point of line $L_{1}, L_{2} and L_{3}$ is given by $(λ - 2, λ + 1, λ)$ , $(5 μ + 3, - μ, μ + 1)$ and $(- 3 δ, 3 δ + 3, δ + 2)$ respectively.

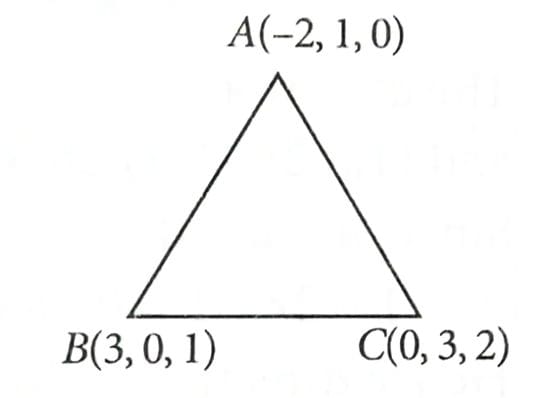
Point of intersection of $L_{1}$ and $L_{2}$ is given by

$\begin{matrix} λ - 2 = 5 μ + 3 \\ λ + 1 = - μ \\ λ = μ + 1 \end{matrix}} \Rightarrow λ = 0, μ = - 1$

$∴$ Point of intersection is A(–2, 1, 0).

Point of intersection of $L_{2}$ and $L_{3}$ is given by

$\begin{matrix} 5 μ + 3 = - 3 δ \\ - μ = 3 δ + 3 \\ μ + 1 = δ + 2 \end{matrix}} \Rightarrow μ = 0, δ = - 1$

$∴$ Point of intersection is B(3, 0 , 1).

Point of intersection of $L_{1}$ and $L_{3}$ is given by

$\begin{matrix} λ - 2 = - 3 δ \\ λ + 1 = 3 δ + 3 \\ λ = δ + 2 \end{matrix}} \Rightarrow λ = 2, δ = 0$

$∴$ Point of intersection is C(0, 3, 2).

Now, Area of $△ A B C = \frac{1}{2}$ $| \vec{A B} \times \vec{B C} |$

$∴ A = \frac{1}{2}$ $| | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ - 5 & 1 & - 1 \\ - 3 & 3 & 1 \end{matrix} | |$

$= \frac{1}{2} | 4 \hat{i} + 8 \hat{j} - 12 \hat{k |}$

$= \frac{1}{2} \sqrt{16 + 64 + 144} = \sqrt{56}$

$∴ A^{2} = 56$ .

Q 73 :

Let $L_{1} : \frac{x - 1}{3} = \frac{y - 1}{- 1} = \frac{z + 1}{0}$ and $L_{2} : \frac{x - 2}{2} = \frac{y}{0} = \frac{z + 4}{α}, α \in R$ be two lines, which intersect at the point B. If P is the foot of perpendicular from the point A(1, 1, –1) and $L_{2}$ , then the value of $26 α {(P B)}^{2}$ is __________. [2025]

0%

(216)

Point $B \equiv (3 μ + 1, - μ + 1, - 1) \equiv (2 λ + 2, 0, α λ - 4)$

$\Rightarrow 3 μ + 1 = 2 λ + 2, - μ + λ = 0, λ α - 4 = - 1$

$∴ μ = 1 \Rightarrow λ = 1 and α = 3$

So, point B(4, 0, –1).

Let point P is (2k + 2, 0, 3k – 4).

So, Dr's of AP is < 2k + 1, –1, 3k – 3 >

Since, $L_{2} ⊥ A P$

$\Rightarrow 2 (2 k + 1) + 0 (- 1) + 3 (3 k - 3) = 0$

$\Rightarrow 4 k + 2 + 9 k - 9 = 0 \Rightarrow k = \frac{7}{13}$

$∴ Point P \equiv (\frac{40}{13}, 0, \frac{- 31}{13})$

$∴ {(P B)}^{2} = {(\frac{40}{13} - 4)}^{2} + {(0 - 0)}^{2} + {(\frac{- 31}{13} + 1)}^{2} = \frac{468}{169}$

$∴ 26 α {(P B)}^{2} = 26 \times 3 \times \frac{468}{169} = 216$ .

Q 74 :

Let P be the image of the point Q(7, –2, 5) in the line $L : \frac{x - 1}{2} = \frac{y + 1}{3} = \frac{z}{4}$ and R(5, p, q) be a point on L. Then the square of the area of $∆ PQR$ is __________. [2025]

0%

(957)

Given, $\frac{x - 1}{2} = \frac{y + 1}{3} = \frac{z}{4}$ and R(5, p, q) be on the line.

Here P be the image of point.

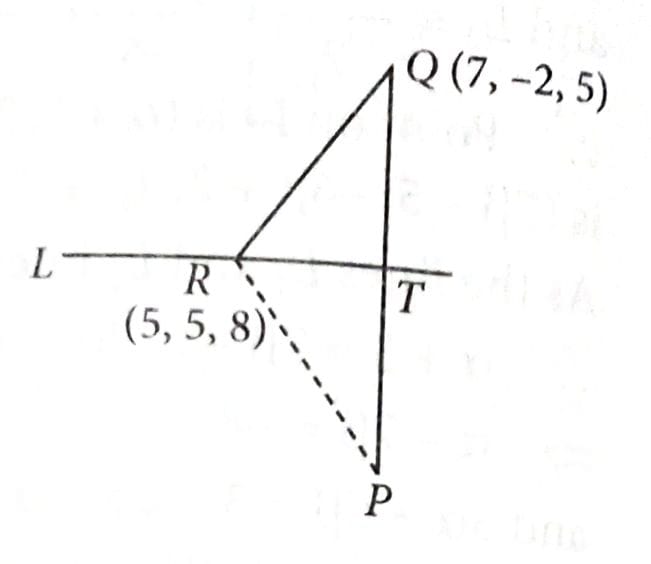
Since, R is on the line L, then

$R \equiv (2 λ + 1, 3 λ - 1, 4 λ) = (5, p, q) [Given]$

$\Rightarrow 2 λ + 1 = 5$

$\Rightarrow 2 λ = 4 \Rightarrow λ = 2$

$∴ R \equiv (5, 5, 8)$

Since, T is also on the line L, then

$T \equiv (2 μ + 1, 3 μ - 1, 4 μ)$

Now, $\vec{Q T} = (2 μ - 6) \hat{i} + (3 μ + 1) \hat{j} + (4 μ - 5) \hat{k}$

and $\vec{b} = 2 \hat{i} + 3 \hat{j} + 4 \hat{k}$ (Normal)

Taking $\vec{Q T} \cdot \vec{b} = 0$

$\Rightarrow 4 μ - 12 + 9 μ + 3 + 16 μ - 20 = 0 \Rightarrow 29 μ - 29 = 0$

$\Rightarrow μ = 1$

$∴ T \equiv (3, 2, 4)$

$\Rightarrow Q T = \sqrt{{(7 - 3)}^{2} + {(- 2 - 2)}^{2} + {(5 - 4)}^{2}}$

$= \sqrt{16 + 16 + 1} = \sqrt{33} \Rightarrow P Q = 2 \sqrt{33}$

Similarly, $R T = \sqrt{29}$

$\Rightarrow Area of △ P Q R = \frac{1}{2} \times \sqrt{29} \times 2 \sqrt{33} = \sqrt{29} \times \sqrt{33}$

$\Rightarrow {(Area of △ P Q R)}^{2} = {(\sqrt{29} \times \sqrt{33})}^{2} = 29 \times 33 = 957$ .

Q 75 :

The shortest distance between the lines $\frac{x - 4}{4} = \frac{y + 2}{5} = \frac{z + 3}{3}$ and $\frac{x - 1}{3} = \frac{y - 3}{4} = \frac{z - 4}{2}$ is [2023]

$3 \sqrt{6}$
$6 \sqrt{2}$
$2 \sqrt{6}$
$6 \sqrt{3}$

1

2

3

4

(1)

$We have,$ $l_{1} : \frac{x - 4}{4} = \frac{y + 2}{5} = \frac{z + 3}{3},$ $l_{2} : \frac{x - 1}{3} = \frac{y - 3}{4} = \frac{z - 4}{2}$

$Here, x_{1} = 4, y_{1} = - 2, z_{1} = - 3, a_{1} = 4, b_{1} = 5, c_{1} = 3$

$x_{2} = 1, y_{2} = 3, z_{2} = 4, a_{2} = 3, b_{2} = 4, c_{2} = 2$

$Shortest distance,$ $d =$ $| \frac{| \begin{matrix} x_{2} - x_{1} & y_{2} - y_{1} & z_{2} - z_{1} \\ a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \end{matrix} |}{\sqrt{{(a_{1} b_{2} - a_{2} b_{1})}^{2} + {(b_{1} c_{2} - b_{2} c_{1})}^{2} + {(c_{1} a_{2} - c_{2} a_{1})}^{2}}} |$

$= \frac{| \begin{matrix} 1 - 4 & 3 + 2 & 4 + 3 \\ 4 & 5 & 3 \\ 3 & 4 & 2 \end{matrix} |}{\sqrt{{(4 \times 4 - 3 \times 5)}^{2} + {(5 \times 2 - 4 \times 3)}^{2} + {(3 \times 3 - 4 \times 2)}^{2}}}$

$= \frac{18}{\sqrt{6}} = 3 \sqrt{6}$

Q 76 :

The shortest distance between the lines $\frac{x + 2}{1} = \frac{y}{- 2} = \frac{z - 5}{2}$ and $\frac{x - 4}{1} = \frac{y - 1}{2} = \frac{z + 3}{0}$ is [2023]

9
6
8
7

1

2

3

4

(1)

Q 77 :

Let S be the set of all values of $λ$ , for which the shortest distance between the lines $\frac{x - λ}{0} = \frac{y - 3}{4} = \frac{z + 6}{1}$ and $\frac{x + λ}{3} = \frac{y}{- 4} = \frac{z - 6}{0}$ is 13. Then $8$ $| \sum_{λ \in S} λ |$ is equal to [2023]

302
306
308
304

1

2

3

4

(2)

$Shortest distance between lines$

$\frac{x - λ}{0} = \frac{y - 3}{4} = \frac{z + 6}{1}$ and $\frac{x + λ}{3} = \frac{y}{- 4} = \frac{z - 6}{0}$ is 13

So, $| \frac{| \begin{matrix} λ + λ & 3 - 0 & - 6 - 6 \\ 0 & 4 & 1 \\ 3 & - 4 & 0 \end{matrix} |}{\sqrt{{(0 + 4)}^{2} + {(3 - 0)}^{2} + {(0 - 12)}^{2}}} |$ $= 13$

$\Rightarrow$ $| \frac{| \begin{matrix} 2 λ & 3 & - 12 \\ 0 & 4 & 1 \\ 3 & - 4 & 0 \end{matrix} |}{13} |$ $= 13$

$\Rightarrow$ $| 2 λ (0 + 4) - 3 (- 3) - 12 (0 - 12) |$ $= 13 \times 13$

$\Rightarrow$ $| 8 λ + 9 + 144 |$ $= 169$ $\Rightarrow$ $| 8 λ + 153 |$ $= 169$

$\Rightarrow 8 λ + 153 = 169$ and $8 λ + 153 = - 169 \Rightarrow λ = 2, \frac{- 161}{4}$

$∴$ $8$ $| \sum_{λ \in S} λ |$ $= 8$ $| \frac{- 161}{4} + 2 |$ $= 8$ $| \frac{- 153}{4} |$ $= 153 \times 2 = 306$

Q 78 :

The shortest distance between the lines $\frac{x - 5}{1} = \frac{y - 2}{2} = \frac{z - 4}{- 3}$ and $\frac{x + 3}{1} = \frac{y + 5}{4} = \frac{z - 1}{- 5}$ is [2023]

$7 \sqrt{3}$
$6 \sqrt{3}$
$4 \sqrt{3}$
$5 \sqrt{3}$

1

2

3

4

(2)

Q 79 :

Consider the lines $L_{1}$ and $L_{2}$ given by $L_{1} : \frac{x - 1}{2} = \frac{y - 3}{1} = \frac{z - 2}{2}, L_{2} : \frac{x - 2}{1} = \frac{y - 2}{2} = \frac{z - 3}{3} .$ A line $L_{3}$ having direction ratios $1, - 1, - 2$ intersects $L_{1}$ and $L_{2}$ at the points P and Q respectively. Then the length of line segment PQ is [2023]

$3 \sqrt{2}$
$4$
$2 \sqrt{6}$
$4 \sqrt{3}$

1

2

3

4

(3)

$P lies on \frac{x - 1}{2} = \frac{y - 3}{1} = \frac{z - 2}{2} = λ$

$P \equiv (2 λ + 1, λ + 3, 2 λ + 2)$

$Q lies on \frac{x - 2}{1} = \frac{y - 2}{2} = \frac{z - 3}{3} = μ$

$Q \equiv (μ + 2, 2 μ + 2, 3 μ + 3)$

$D.R.'s of P Q = (2 λ - μ - 1, λ - 2 μ + 1, 2 λ - 3 μ - 1)$

$which are proportional to 1, - 1, - 2$

$\frac{2 λ - μ - 1}{1} = \frac{λ - 2 μ + 1}{- 1} = \frac{2 λ - 3 μ - 1}{- 2}$

$- 2 λ + μ + 1 = λ - 2 μ + 1 \Rightarrow λ = μ$

$- 2 λ + 4 μ - 2 = - 2 λ + 3 μ + 1 \Rightarrow μ = 3 = λ$

$P = (7, 6, 8), Q = (5, 8, 12)$

$P Q^{2} = 2^{2} + 2^{2} + 4^{2} = 24 \Rightarrow P Q = 2 \sqrt{6}$

Q 80 :

The shortest distance between the lines $x + 1 = 2 y = - 12 z$ and $x = y + 2 = 6 z - 6$ is [2023]

$\frac{3}{2}$
$3$
$2$
$\frac{5}{2}$

1

2

3

4

Topic Question Set

Q 72 :

Let the area of the triangle formed by the lines x + 2 = y – 1 = z, $\frac{x - 3}{5} = \frac{y}{- 1} = \frac{z - 1}{1}$ and $\frac{x}{- 3} = \frac{y - 3}{3} = \frac{z - 2}{1}$ be A. Then $A^{2}$ is equal to __________. [2025]

0%

0%

Q 74 :

Let P be the image of the point Q(7, –2, 5) in the line $L : \frac{x - 1}{2} = \frac{y + 1}{3} = \frac{z}{4}$ and R(5, p, q) be a point on L. Then the square of the area of $∆ PQR$ is __________. [2025]

0%

Q 75 :

The shortest distance between the lines $\frac{x - 4}{4} = \frac{y + 2}{5} = \frac{z + 3}{3}$ and $\frac{x - 1}{3} = \frac{y - 3}{4} = \frac{z - 4}{2}$ is [2023]

Q 76 :

The shortest distance between the lines $\frac{x + 2}{1} = \frac{y}{- 2} = \frac{z - 5}{2}$ and $\frac{x - 4}{1} = \frac{y - 1}{2} = \frac{z + 3}{0}$ is [2023]

(1)

Q 77 :

Let S be the set of all values of $λ$ , for which the shortest distance between the lines $\frac{x - λ}{0} = \frac{y - 3}{4} = \frac{z + 6}{1}$ and $\frac{x + λ}{3} = \frac{y}{- 4} = \frac{z - 6}{0}$ is 13. Then $8$ $| \sum_{λ \in S} λ |$ is equal to [2023]

Q 78 :

The shortest distance between the lines $\frac{x - 5}{1} = \frac{y - 2}{2} = \frac{z - 4}{- 3}$ and $\frac{x + 3}{1} = \frac{y + 5}{4} = \frac{z - 1}{- 5}$ is [2023]

(2)

Q 80 :

The shortest distance between the lines $x + 1 = 2 y = - 12 z$ and $x = y + 2 = 6 z - 6$ is [2023]

(3)

Want Us to Email you About Special Offers & Updates?

Topic Question Set

0%

0%

0%

(1)

(2)

Q 80 : The shortest distance between the lines x+1=2y=-12z and x=y+2=6z-6 is [2023] .question-row { display: flex; align-items: flex-start; gap: 8px; } .q-no { font-size: 17px; white-space: nowrap; margin-left: -15px; } .q-text { font-size: 18px; flex: 1; } .q-no, .q-text p { line-height: 30px; }

(3)

Want Us to Email you About Special Offers & Updates?

Q 80 :

The shortest distance between the lines $x + 1 = 2 y = - 12 z$ and $x = y + 2 = 6 z - 6$ is [2023]