(1)

The given lines are $L_1:\frac{x–1}{2}=\frac{y–2}{3}=\frac{z–3}{4}$ and $L_2:\frac{x}{1}=\frac{y}{\alpha }=\frac{z–5}{1}$,

$\overrightarrow{n}=$$\left|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ 2& 3& 4\\ 1& \alpha & 1\end{array}\right|$

$=\hat{i}(3–4\alpha )–\hat{j}(2–4)+\hat{k}(2\alpha –3)$

$=\hat{i}(3–4\alpha )–\hat{j}(–2)+\hat{k}(2\alpha –3)$

Shortest distance = $\left|\frac{\overrightarrow{BA}·\overrightarrow{n}}{\left|\overrightarrow{n}\right|}\right|$$=$$\left|\frac{(\hat{i}+2\hat{j}–2\hat{k})·\overrightarrow{n}}{\left|\overrightarrow{n}\right|}\right|$$=\frac{5}{\sqrt{6}}$          [Given]

$=$$\left|\frac{13–8\alpha }{\sqrt{{(3–4\alpha )}^2+4+{(2\alpha –3)}^2}}\right|$$=\frac{5}{\sqrt{6}}$

$\Rightarrow 6{(13–8\alpha )}^2=25({(4\alpha –3)}^2+{(2\alpha –3)}^2+4)$

$\Rightarrow 6(64{\alpha }^2–208\alpha +169)=\left(25\right(20{\alpha }^2–36\alpha +22\left)\right)$

$\Rightarrow 116{\alpha }^2+348\alpha –464=0$

$\therefore$   Sum of roots ${\alpha }_1$ and ${\alpha }_2=\frac{–348}{116}=–3$.

(3)

Equation of line L passes through (1, 1, 1) is $L:\frac{x–1}{a}=\frac{y–1}{b}=\frac{z–1}{c}$, where a, b, c are direction ratios.

Let $L_1:\frac{x–1}{2}=\frac{y+1}{3}=\frac{z–1}{4}=\lambda \left(\mathrm{say}\right)$

Any point on $L_1$ be $A(2\lambda +1,3\lambda –1,4\lambda +1)$

Let $L_2:\frac{x–3}{1}=\frac{y–4}{2}=\frac{z}{1}=\mu \left(\mathrm{say}\right)$

Any point on $L_2$ be $B(\mu +3,2\mu +4,\mu )$

Direction ratio of L be : $<2\lambda ,3\lambda –2,4\lambda > \mathrm{or} <\mu +2,2\mu +3,\mu –1>$

Now, $\frac{2\lambda }{\mu +2}=\frac{3\lambda –2}{2\mu +3}=\frac{4\lambda }{\mu –1} \Rightarrow \lambda =\frac{–6}{5} \mathrm{and} \mu =–5$

$\therefore <a,b,c>\equiv <–3,–7,–6> \mathrm{or} <3,7,6>$

$\therefore L:\frac{x–1}{3}=\frac{y–1}{7}=\frac{z–1}{6}$

Hence, (7, 15, 13) lies on the line.

(3)

Since, given line is perpendicular to both the line, i.e., $(\hat{i}+a\hat{j}+b\hat{k})\times (–b\hat{i}+a\hat{j}+5\hat{k})$

Also, parallel vector along the required line is

     $(\hat{i}+a\hat{j}+b\hat{k})\times (–b\hat{i}+a\hat{j}+5\hat{k})$

$=(5a–ab)\hat{i}–(b^2+5)\hat{j}+(a+ab)\hat{k}$

$\therefore$   Dr's of required lines are $(5a–ab), –(b^2+5), (a+ab)$

But given Dr's of required line are –2, d, –4

$\therefore \frac{5a–ab}{–2}=\frac{–(b^2+5)}{d}=\frac{a+ab}{–4}$          ... (i)

Since, point $(0,\frac{–1}{2},0)$ lies on $\frac{x–1}{–2}=\frac{y+4}{d}=\frac{z–c}{–4}$,

$\Rightarrow \frac{0–1}{–2}=\frac{{\displaystyle \frac{–1}{2}}+4}{d}=\frac{0–c}{–4} \Rightarrow d=7, c=2$

From (i), $\frac{5a–ab}{–2}=\frac{–b^2–5}{7}=\frac{a+ab}{–4}$

$\begin{array}{c}\frac{5a-ab}{-2}=\frac{a+ab}{-4}\\ \Rightarrow -20a+4ab=-2a-2ab\\ \Rightarrow 18a=6ab\\ \Rightarrow b=3\end{array}|$$\begin{array}{c}\frac{-b^2-5}{7}=\frac{a+ab}{-4}\\ \Rightarrow 4b^2+20=7a+7ab\\ \Rightarrow 36+20=7a+21a\\ \Rightarrow 56=28a\Rightarrow a=2\end{array}$

$\therefore$   a + b + c + d = 2 + 3 + 2 + 7 = 14

(1)

We have, the point P(5, 1, –3)

$L_1$ : x – 1 = y – 2 = z = $\lambda$ (say)

$L_2$ : x – 2 = y = z – 1 = $\mu$ (say)

Any point on $L_1$ and $L_2$ are given by $Q(\lambda +1,\lambda +2,\lambda )$ and $R(\mu +2,\mu ,\mu +1)$ respectively.

       $\overrightarrow{PQ}=(\lambda –4)\hat{i}+(\lambda +1)\hat{j}+(\lambda +3)\hat{k}$

Since, $\overrightarrow{PQ}\perp L_1$, whose direction ratios are < 1, 1, 1 >, So we have

       $1(\lambda –4)+1(\lambda +1)+1(\lambda +3)=0$

$\Rightarrow 3\lambda =0 \Rightarrow \lambda =0$

$\therefore$   Q(1, 2, 0) is the foot of perpendicular on $L_1$. Similarly,

       $\overrightarrow{PR}=(\mu –3)\hat{i}+(\mu –1)\hat{j}+(\mu +4)\hat{k}$

Now, $\overrightarrow{PQ}\perp L_2$, whose direction ratios are < 1, 1, 1 >, so we have

      $1(\mu –3)+1(\mu –1)+1(\mu +4)=0$

$\Rightarrow 3\mu –4+4=0 \Rightarrow \mu =0$

$\therefore$   R(2, 0, 1) is foot of perpendicular on $L_2$.

Now, area $△PQR=\frac{1}{2}$$|\overrightarrow{PQ}\times \overrightarrow{PR}|$

$\Rightarrow A=\frac{1}{2}$$\left|\right|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ –4& 1& 3\\ –3& –1& 4\end{array}\left|\right|$$=\frac{1}{2}$$|7\hat{i}+7\hat{j}+7\hat{k}|$$=\frac{7\sqrt{3}}{2}$

$\therefore 4A^2=4\times {(\frac{1}{2}\times 7\sqrt{3})}^2=147$

(4)

$\overrightarrow{a}=2\hat{i}+3\hat{j}+4\hat{k} \mathrm{and} \overrightarrow{b}=3\hat{i}+4\hat{j}+5\hat{k}$

represents direction vector of the given lines.

$\therefore \overrightarrow{a}\times \overrightarrow{b}=$$\left|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ 2& 3& 4\\ 3& 4& 5\end{array}\right|$

$=\hat{i}(15–16)–\hat{j}(10–12)+\hat{k}(8–9)=–\hat{i}+2\hat{j}–\hat{k}$

The given lines passes through ${\overrightarrow{p}}_1=\hat{i}+2\hat{j}+3\hat{k}$ and ${\overrightarrow{p}}_2=\lambda \hat{i}+4\hat{j}+5\hat{k}$

$\therefore {\overrightarrow{p}}_2–{\overrightarrow{p}}_1=(\lambda –1)\hat{i}+2\hat{j}+2\hat{k}$

Shortest distance between given lines $=$$\left|\frac{({\overrightarrow{p}}_2–{\overrightarrow{p}}_1)·(\overrightarrow{a}\times \overrightarrow{b})}{|\overrightarrow{a}\times \overrightarrow{b}|}\right|$

$\Rightarrow \frac{1}{\sqrt{6}}=$$\left|\frac{–\lambda +1+4–2}{\sqrt{1+4+1}}\right|$

$\Rightarrow$$|–\lambda +3|$$=1 \Rightarrow \lambda =3\pm 1 \Rightarrow \lambda =4,2$

Radius of circle passing through points (0, 0), (4, 2), (2, 4) is given by $\frac{abc}{4△}$.

$=\frac{\sqrt{20}\times \sqrt{20}\times \sqrt{8}}{4\times {\displaystyle \frac{1}{2} \left|\begin{array}{ccc}1& 1& 1\\ 0& 4& 2\\ 0& 2& 4\end{array}\right|}}=\frac{20\times 2\sqrt{2}}{2\times 12}=\frac{5\sqrt{2}}{3}$

(3)

We have, $L_1:\frac{x–1}{2}=\frac{y–2}{3}=\frac{z–3}{4}$ and $L_2:\frac{x–2}{3}=\frac{y–4}{4}=\frac{z–5}{5}$

Let $A(2\lambda +1,3\lambda +2,4\lambda +3)$ and $B(3\mu +2,4\mu +4,5\mu +5)$ lies on the line $L_1$ and $L_2$ respectively.

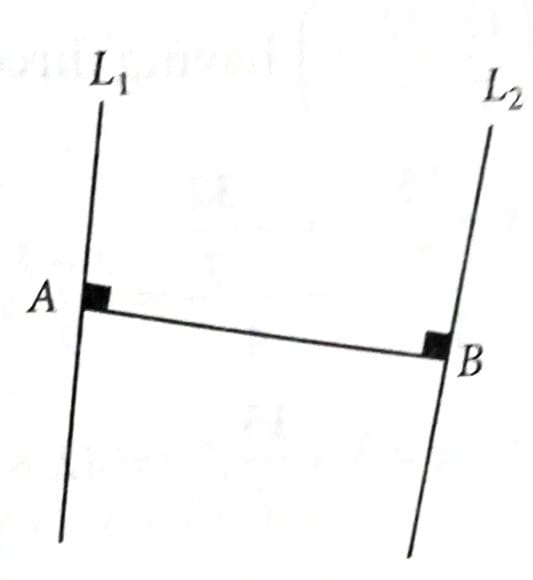
Direction ratios of AB is

$<3\mu –2\lambda +1,4\mu –3\lambda +2,5\mu –4\lambda +2>$

As $AB\perp L_1$, we have

$2(3\mu –2\lambda +1)+3(4\mu –3\lambda +2)+4(5\mu –4\lambda +2)=0$

$\Rightarrow 6\mu –4\lambda +2+12\mu –9\lambda +6+20\mu –16\lambda +8=0$

$\Rightarrow 38\mu –29\lambda +16=0$          ... (i)

Also, $AB\perp L_2$, we have

$3(3\mu –2\lambda +1)+4(4\mu –3\lambda +2)+5(5\mu –4\lambda +2)=0$

$\Rightarrow 50\mu –38\lambda +21=0$          ... (ii)

Solving (i) and (ii), we get

$\lambda =\frac{1}{3} \mathrm{and} \mu =\frac{–1}{6}$

$\therefore$   Coordinate of A is $(\frac{5}{3},3,\frac{13}{3})$ and $B(\frac{3}{2},\frac{10}{3},\frac{25}{6})$

Equation of AB is given by

$\frac{x–{\displaystyle \frac{5}{3}}}{{\displaystyle \frac{1}{6}}}=\frac{y–3}{–{\displaystyle \frac{1}{3}}}=\frac{z–{\displaystyle \frac{13}{3}}}{{\displaystyle \frac{1}{6}}} \Rightarrow x–\frac{5}{3}=\frac{y–3}{–2}=z–\frac{13}{3}$

$\therefore$   Point $(\frac{14}{3},–3,\frac{22}{3})$ lies on line AB.

(2)

$\frac{x–1}{2}=\frac{y+2}{–1}=\frac{z+3}{2}=\lambda \left(\mathrm{say}\right)$

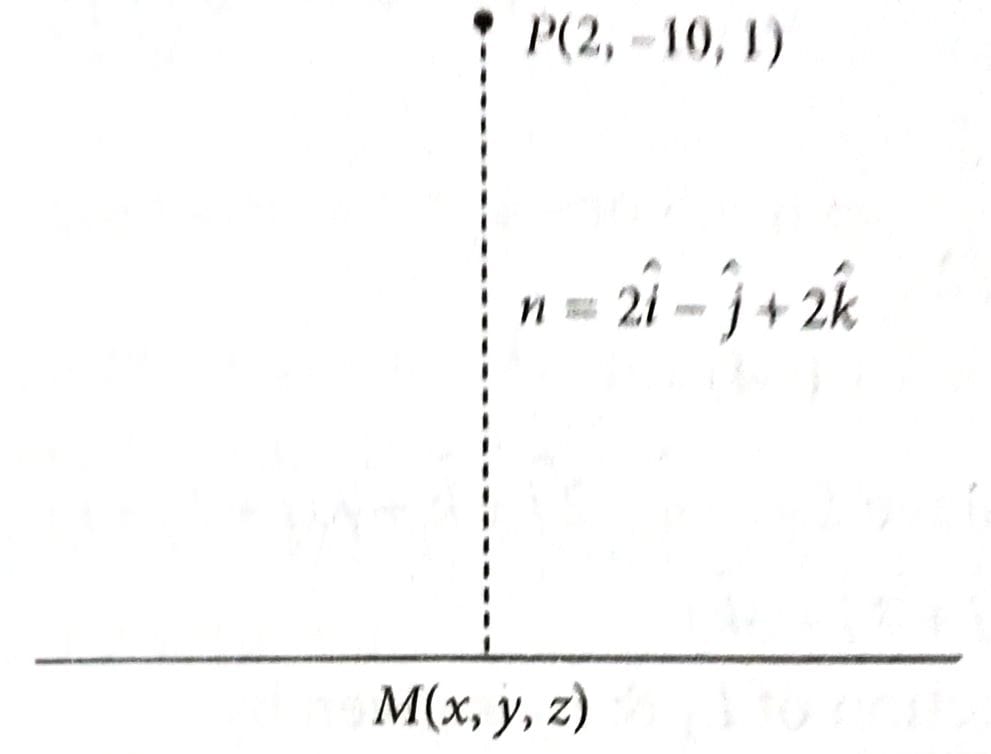
Any point on the line is given by

$M(x,y,z)\equiv (2\lambda +1,–\lambda –2,2\lambda –3)$

Also, $\overrightarrow{PM}=(2\lambda +1–2)\hat{i}+(–\lambda –2+10)\hat{j}+(2\lambda –3–1)\hat{k}$

$=(2\lambda –1)\hat{i}+(–\lambda +8)\hat{j}+(2\lambda –4)\hat{k}$          ... (i)

$\because \overrightarrow{PM}·\overrightarrow{n}=0$

$\Rightarrow (2\lambda –1)2+(–\lambda +8)(–1)+(2\lambda –4)2=0$

$\Rightarrow 4\lambda –2+\lambda –8+4\lambda –8=0$

$\Rightarrow 9\lambda –18=0 \Rightarrow \lambda =2$

$\therefore \left|\overrightarrow{PM}\right|=\sqrt{3^2+6^2+0^2}=\sqrt{45}=3\sqrt{5}$          [Using (i)]

(1)

Equation of line passing through P(–2, –1, 3) and parallel to vector $3\hat{i}+2\hat{j}+2\hat{k}$ is $\frac{x+2}{3}=\frac{y+1}{2}=\frac{z–3}{2}$.

Let $\frac{x+2}{3}=\frac{y+1}{2}=\frac{z–3}{2}=\lambda$

$\Rightarrow Q=(3\lambda –2,2\lambda –1,2\lambda +3), \lambda \in \mathrm{ℝ}–\left\{0\right\}$

Also, $\left|\overrightarrow{QR}\right|$$=5=\sqrt{{(3\lambda –3)}^2+{(2\lambda –4)}^2+{\left(2\lambda \right)}^2}$

$\therefore 17{\lambda }^2–34\lambda +25=25 \Rightarrow \lambda =2 (\because \lambda \ne 0)$

         Q(4, 3, 7), P(–2, –1, 3), R(1, 3, 3)

$\therefore \mathrm{Area} \mathrm{of} △PQR=\frac{1}{2}$$|\overrightarrow{PQ}\times \overrightarrow{PR}|$

$△=\frac{1}{2}$$\left|\right|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ 6& 4& 4\\ 3& 4& 0\end{array}\left|\right|$

$△=$$|–8\hat{i}+6\hat{j}+6\hat{k}|$$=\sqrt{136} \therefore {△}^2=136$

(4)

Let $\frac{x–3}{7}=\frac{y–2}{–1}=\frac{z+1}{–2}=\lambda$ then

Point $P=(7\lambda +3,–\lambda +2,–2\lambda –1)$

Now, Dr's of $QP=(7\lambda –7,–\lambda +5,–2\lambda )$

$\therefore (7\lambda –7)\left(7\right)+(–\lambda +5)(–1)+(–2\lambda )(–2)=0$

$\Rightarrow 49\lambda –49+\lambda –5+4\lambda =0 \Rightarrow \lambda =1$

$\therefore P=(10,1,–3)$

$\therefore \overrightarrow{PQ}=–4\hat{j}+2\hat{k}, \overrightarrow{PR}=–7\hat{i}–3\hat{j}+4\hat{k}$           [$\because$ R = (3, –2, 1)]

$\therefore \mathrm{Area} \mathrm{of} △PQR=\frac{1}{2}$$\left|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ 0& –4& 2\\ –7& –3& 4\end{array}\right|$

                                         $=\frac{1}{2}$$|–10\hat{i}–14\hat{j}–28\hat{k}|$

                                         $=\frac{1}{2}\sqrt{100+196+784}=3\sqrt{30} \mathrm{sq}. \mathrm{units}$.

(4)

We have, ${\overrightarrow{a}}_1=2\hat{i}+\hat{j}–3\hat{k}, {\overrightarrow{b}}_1=\hat{i}+2\hat{j}–3\hat{k}$

${\overrightarrow{a}}_2=–\hat{i}–3\hat{j}–5\hat{k}, {\overrightarrow{b}}_2=2\hat{i}+4\hat{j}–5\hat{k}$

Now, ${\overrightarrow{b}}_1\times {\overrightarrow{b}}_2=$$\left|\begin{array}{ccc}\hat{i}& \hat{j}& \hat{k}\\ 1& 2& –3\\ 2& 4& –5\end{array}\right|$$=2\hat{i}–\hat{j}$

and ${\overrightarrow{a}}_2–{\overrightarrow{a}}_1=–3\hat{i}–4\hat{j}–2\hat{k}$

$\therefore$   The shortest distance (d) between given lines

$=\frac{\left|\right({\overrightarrow{a}}_2–{\overrightarrow{a}}_1)·({\overrightarrow{b}}_1\times {\overrightarrow{b}}_2\left)\right|}{\left|\right({\overrightarrow{b}}_1\times {\overrightarrow{b}}_2\left)\right|} \Rightarrow d=\frac{2}{\sqrt{5}} \Rightarrow d^2=\frac{4}{5}$

$\therefore m=4, n=5 \Rightarrow m+n=9$