Topic Question Set
Q 11
:
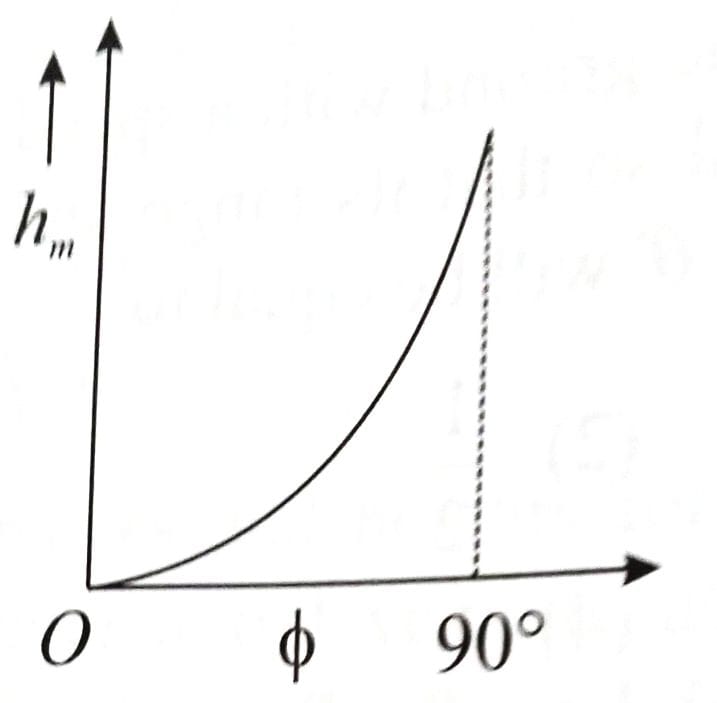
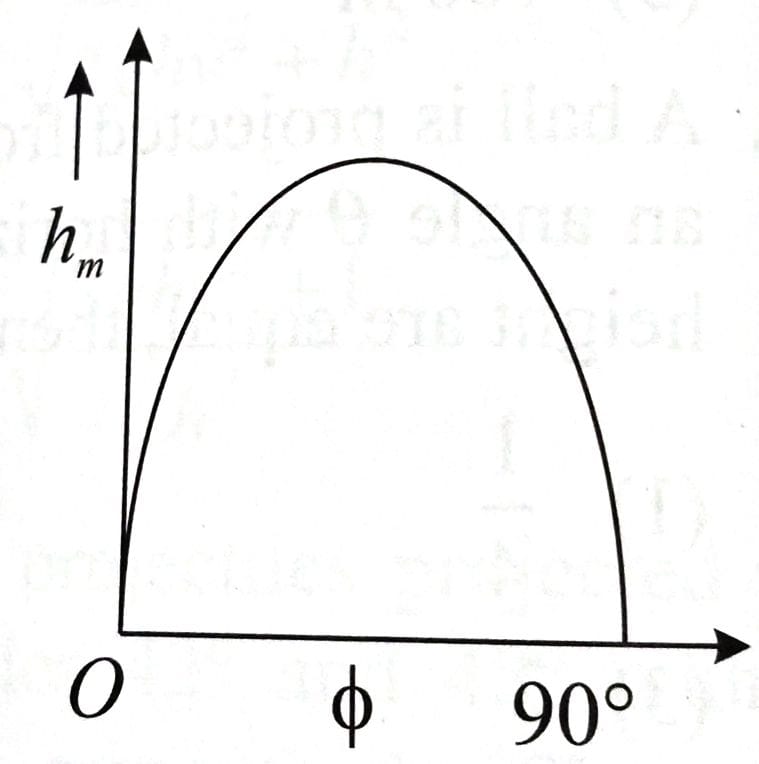
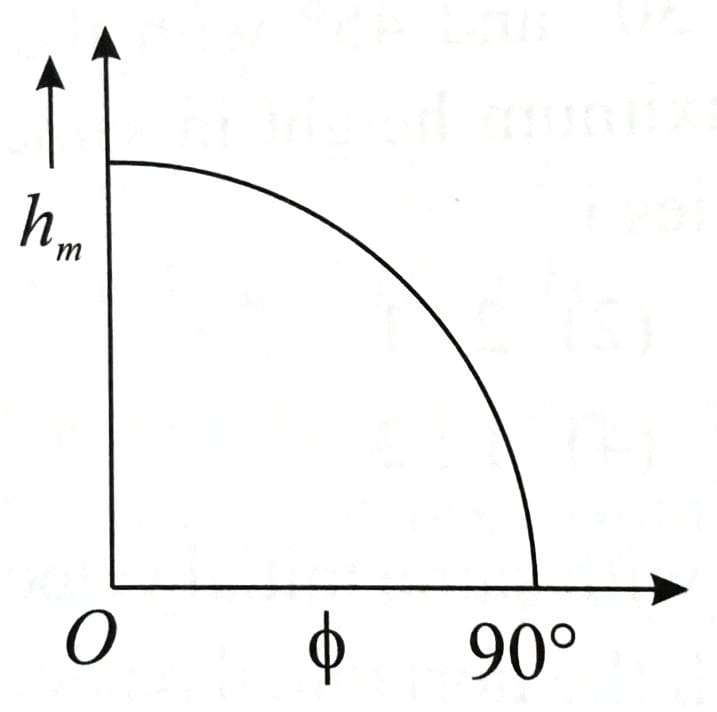
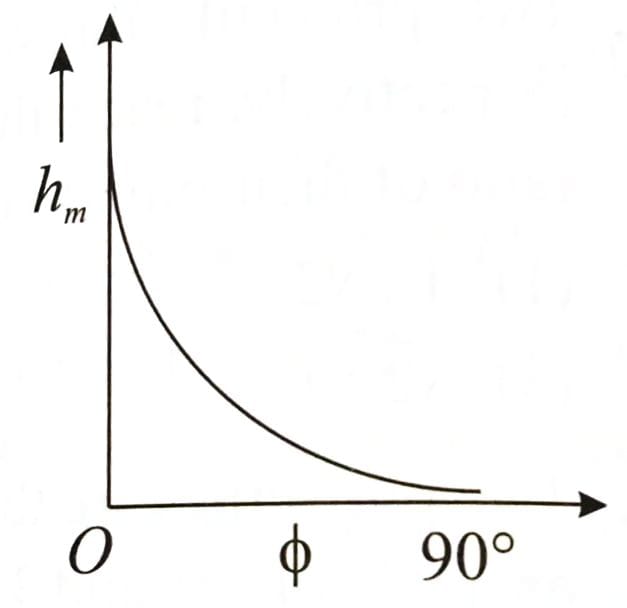
The angle of projection of a particle is measured from the vertical axis as and the maximum height reached by the particle is . Here as function of can be represented as [2025]
(3)
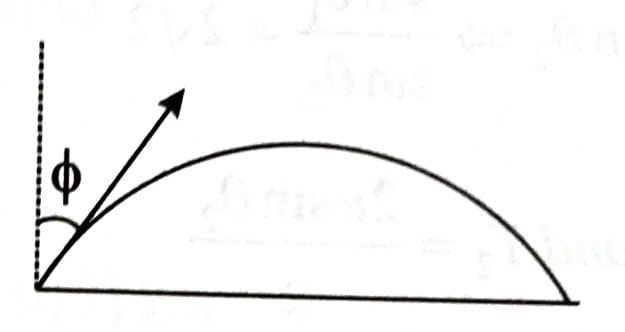
From
decreases with function.
Q 12
:
A particle is projected with velocity so that its horizontal range is three times the maximum height attained by it. The horizontal range of the projectile is given as , where value of n is : (Given 'g' is the acceleration due to gravity). [2025]
6
18
12
24
(4)
Range R =
Q 13
:
Two projectiles are fired from ground with same initial speeds from same point at angles (45° + ) and (45° – ) with horizontal direction. The ratio of their times of flights is [2025]
1
-
-
-
(4)
Time of flight for projectile,
Time of flight for projectile,
Q 14
:
A helicopter flying horizontally with a speed of 360 km/h at an altitude of 2 km, drops an object at an instant. The object hits the ground at a point 'O', 20 s after it is dropped. Displacement of 'O' from the position of helicopter where the object was released is:
(Use acceleration due to gravity g = 10 and neglect air resistance) [2025]
km
4 km
7.2 km
km
(4)
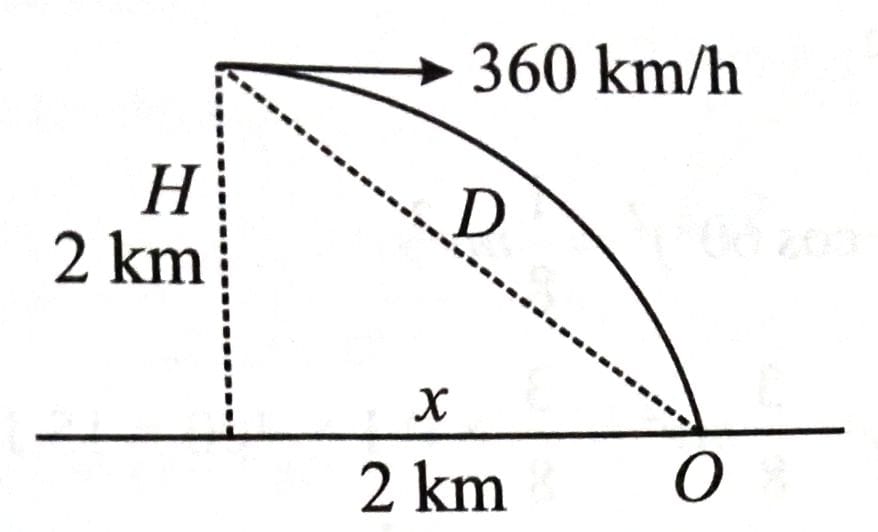
Displacement, .
Q 15
:
Two balls with same mass and initial velocity, are projected at different angles in such a way that maximum height reached by first ball is 8 times higher than that of the second ball. and are the total flying times of first and second ball, respectively, then the ratio of and is : [2025]
-
2 : 1
-
4:1
(1)
Given,
Q 16
:
A particle is projected at an angle of 30° from horizontal at a speed of 60 m/s. The height traversed by the particle in the first second is and height traversed in the last second, before it reaches the maximum height, is . The ratio : is ___________ [Take, g = 10 ] [2025]
(5)
Time to reach maximum height,
Height in second
Height in last second