Topic Question Set
Q 21
:
The area of the region enclosed by the parabola the line and the positive coordinate axes is ____________. [2024]
(5)
Given, equation of parabola
...(i)
and line ...(ii)
From (ii), we have
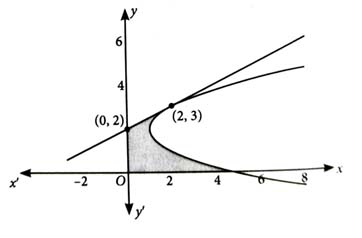
Putting in (i), we get
From (ii), we have,
Intersection point of (i) and (ii) is (2,3).
Q 22
:
The area of the region is [2025]
512
-
-
-
(3)
We have,
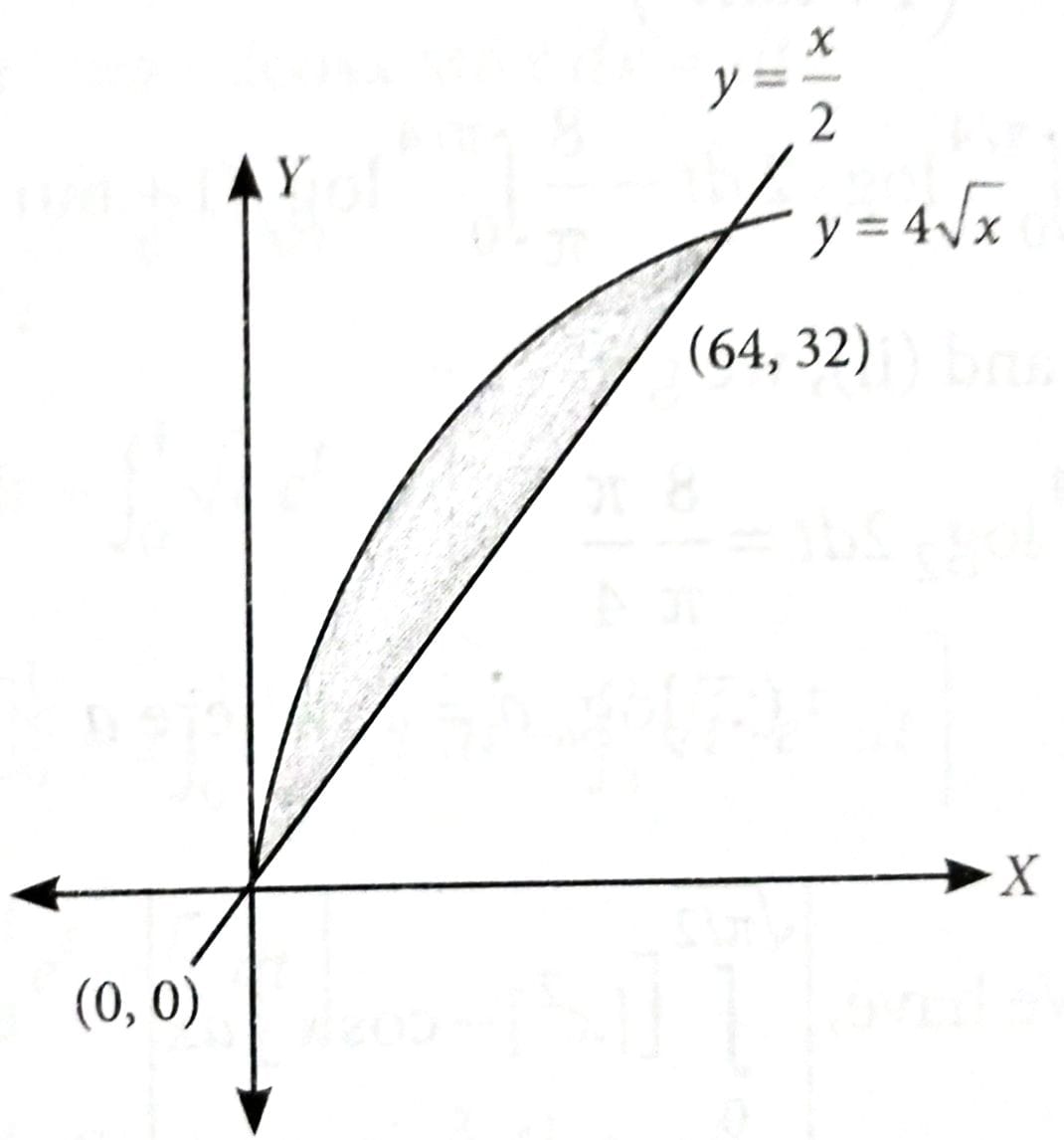
Now,
Required Area
.
Q 23
:
Let be a differentiable function such that for all .
Then the area of the region bounded by y = f(x) and the coordinates axes is [2025]
-
-
-
2
(1)
We have,
This is a linear differential equation, so we have
[]
So, area .
Q 24
:
A line passing through the point A(–2, 0), touches the parabola at the point B in the first quadrant. The area, of the region bounded by the line AB, parabola P and the x-axis, is : [2025]
-
2
3
-
(4)
Given parabola and line is passing through A(–2, 0)
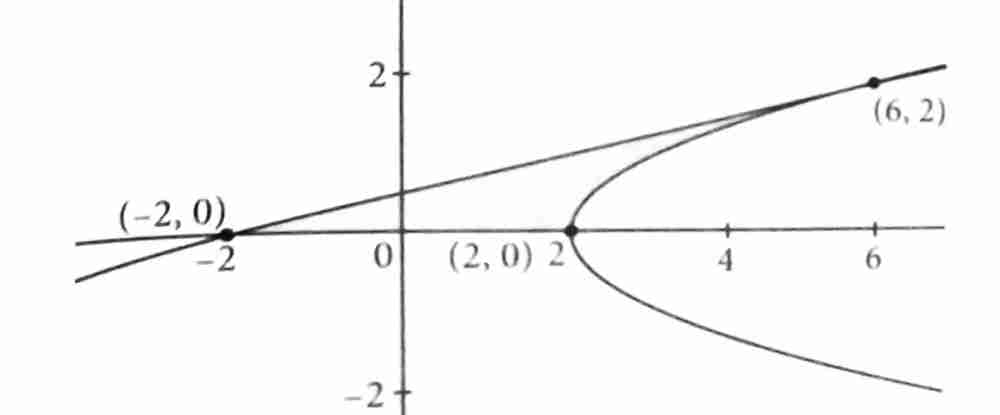
Tangent is y = m(x + 2)
As D = 0
So, tangent is
Point of tangency is (6, 2)
Area of region
sq. units.
Q 25
:
If the area of the region bounded by the curves and is equal to , then equals [2025]
240
220
210
250
(4)
Given, ... (i)
and ... (ii)
From (i) & (ii), we get
x = –6, 4 and y = –5, 0
Thus, point of intersection of (i) & (ii) are (–6, 5) and (4, 0).
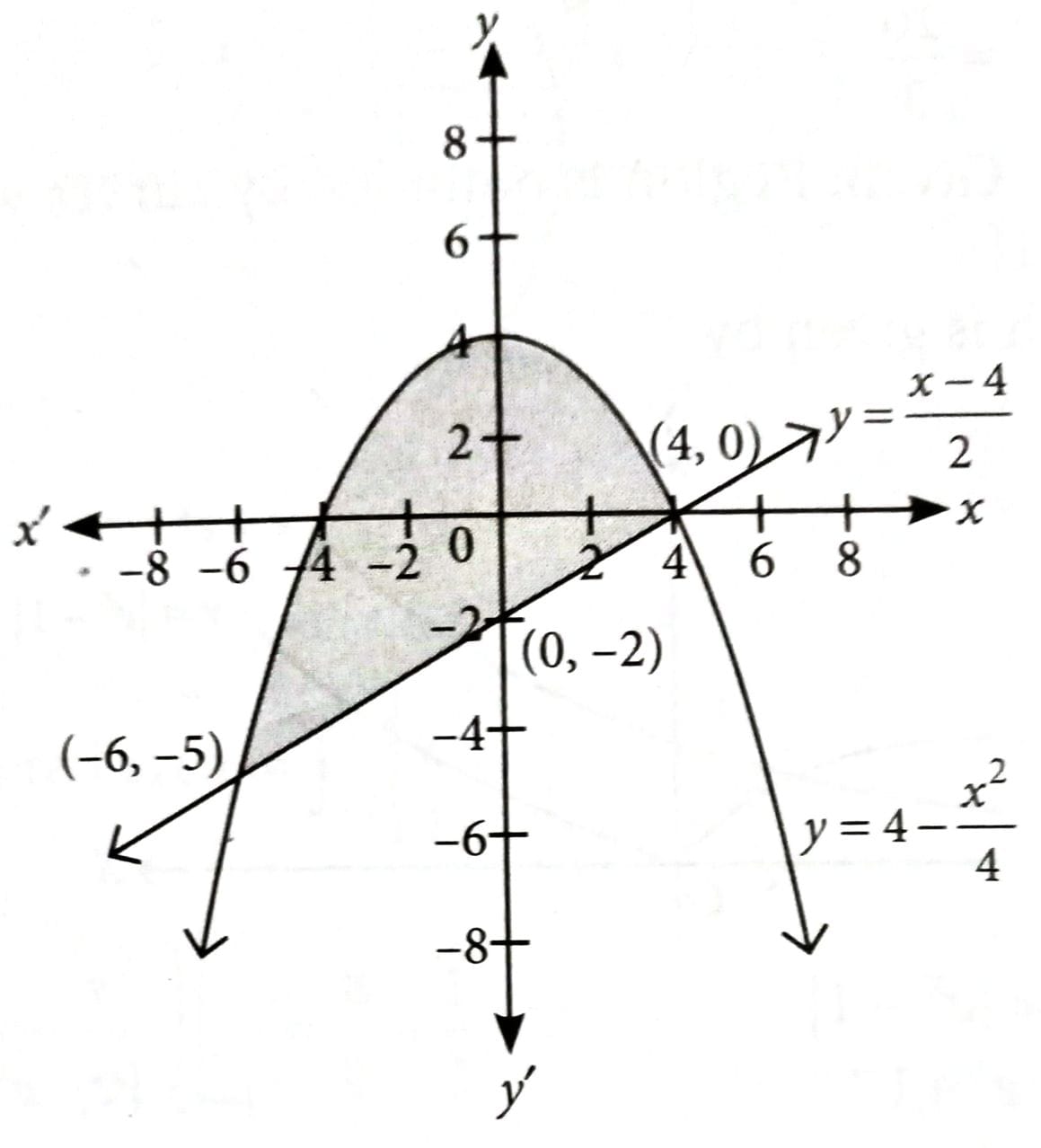
Required Area
.
Q 26
:
If the area of the region is A, then 3A is equal to [2025]
47
49
50
46
(3)
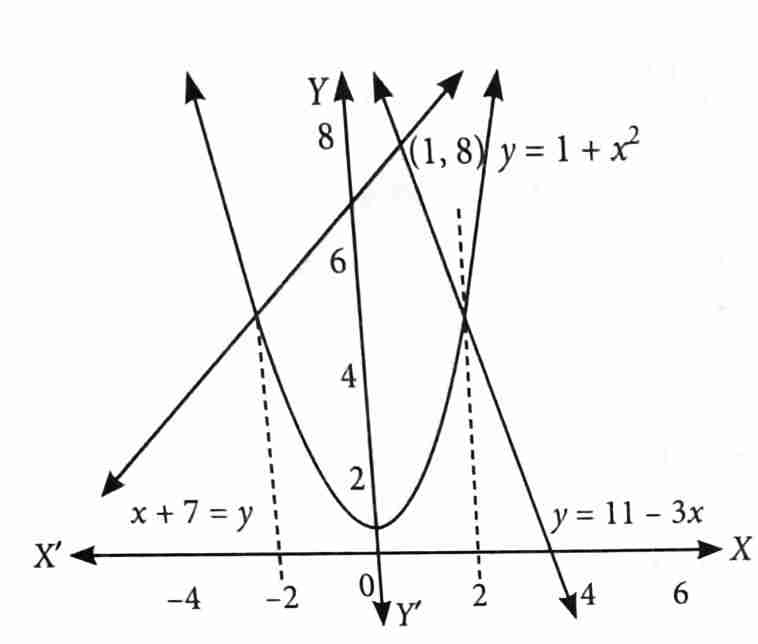
.
Q 27
:
The area of the region, inside the circle and outside the parabola is : [2025]
(3)
We have, , a circle with centre and radius and a parabola .
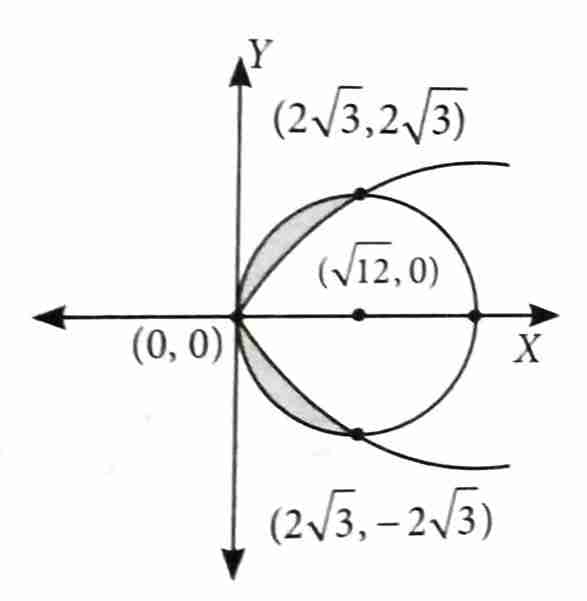
Required Area =
.
Q 28
:
Let be a twice differentiable function such that f(x + y) = f(x)f(y) for all x, . If and f satisfies , a > 0, then the area of the region is : [2025]
(2)
We have, f(x + y) = f(x)f(y)
Let
Differentiating w.r.t. x, we get
Put x = 0, we get
[]
So,
Now,
[]
Now,
Area of region .
Q 29
:
The area of the region enclosed by the curves and is : [2025]
5
4/3
8/3
8
(3)
The given curves are and
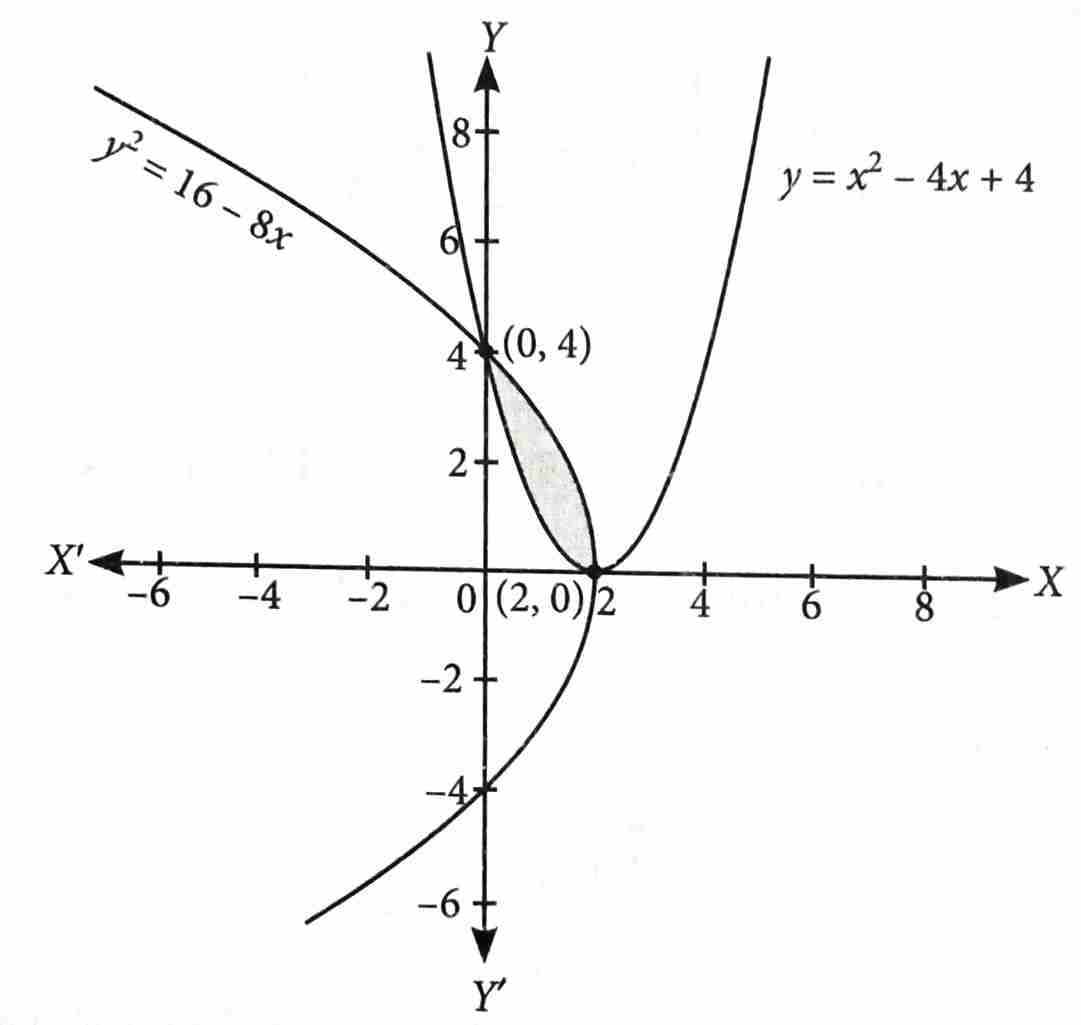
Points of intersection are (2, 0) and (0, 4).
Required Area
sq. units.
Q 30
:
If the area of the region is , then the value of a is : [2025]
6
8
7
5
(4)
Required area
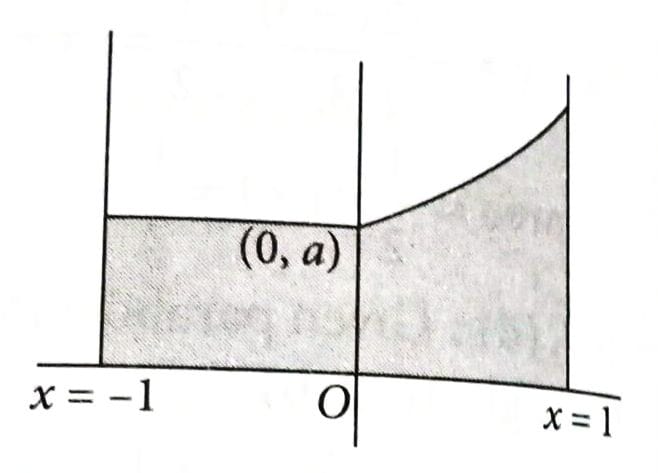
.

