Topic Question Set
Q 1
:
If the area of the region is then the value of is equal to : [2024]
2
- 1
1
0
(2)
Area of region
Q 2
:
The area (in square units) of the region enclosed by the ellipse in the first quadrant below the line is [2024]
(1)
We have,
For point of intersection of ellipse and line we have,
Required area
Q 3
:
Three points are on the parabola Let be the area of the region bounded by the line PQ and the parabola, and be the area of the triangle If the minimum value of is then is equal to _______ . [2024]
(7)
Equation of line is,
...(i)
Also,
Q 4
:
The sum of squares of all possible values of for which area of the region bounded by the parabolas and is maximum, is equal to _______ . [2024]
(8)
and
Point of intersection
Q 5
:
One of the points of intersection of the curves and is Let the area of the region enclosed by these curves be where Then is equal to [2024]
32
30
29
31
(2)
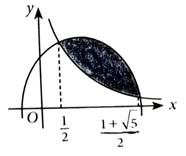
Given curves are
On solving,
Required Area =
[Given]
and
Hence,
Q 6
:
The area (in sq. units) of the region described by is [2024]
(3)
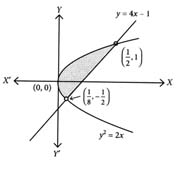
Q 7
:
The area enclosed between the curves and is: [2024]
(3)
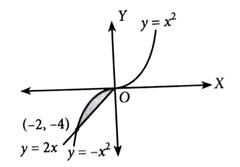
Q 8
:
Let the area of the region enclosed by the curves be Then 10A is equal to [2024]
162
184
154
172
(1)
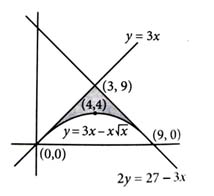
Required area,
So,
Q 9
:
The area of the region in the first quadrant inside the circle and outside the parabola is equal to: [2024]
(4)
We have,
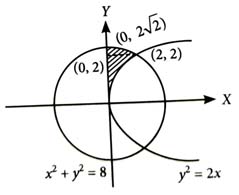
Required area = area of the shaded region
Q 10
:
The parabola divides the area of the circle in two parts. The area of the smaller part is equal to : [2024]
(3)
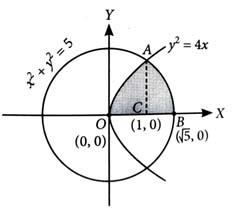
The points of intersection of and are (1, 2) and (1, -2).

