Topic Question Set
Q 21
:
Let be a thrice differentiable function such that Then, the minimum number of zeros of is _______ . [2024]
(5)
Q 22
:
Let denote the greatest integer less than or equal to Let be a function defined by Let be the set of all points in the interval [0, 8] at which is not continuous. Then is equal to ______ . [2024]
(17)
Given,
Q 23
:
Let be a function given by
[2024]
(81)
Hence,
Q 24
:
For a differentiable function suppose where and Then is equal to ______ . [2024]
(61)
We have
Let and
Now, so
[Putting value of in eq. (i)]
Now,
So,
Q 25
:
If then is equal to _______ . [2024]
(105)
We have,
Q 26
:
[2024]
(2890)
...(i)
Now,
..(ii)
Now, [Using (i)]
Q 27
:
[2024]
(202)
Now,
Q 28
:
If the function is differentiable on then is equal to ______ . [2024]
(15)
Since, is differentiable so must be continuity
...(i)
Also, is differentiable at
Now, around 2,
Now, R.H.D. at L.H.D. at
So,
Q 29
:
Let If and denote the number of points where is not continuous and not differentiable respectively, then is equal to [2024]
5
3
2
0
(2)
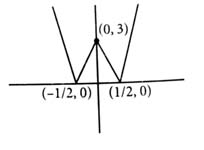
We have,
is continuous at every point.
So,
Now, from the graph, is non-differentiable at
So,
Q 30
:
Consider the function defined by and the function defined by
Then, [2024]
is neither continuous nor differentiable at
is continuous and differentiable for all
is continuous but not differentiable at
is not continuous for all
(3)
Given,
and
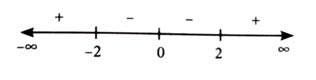
is decreasing in (0, 2).
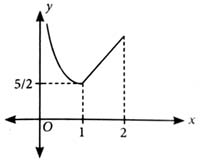
From the graph, we see that is continuous but not differentiable at

