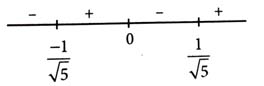Topic Question Set
Q 1
:
For the function consider the following two statements :
(I) is increasing in
(II) is decreasing in .
Between the above two statements, [2024]
neither (I) nor (II) is true.
only (II) is true.
both (I) and (II) are true.
only (I) is true.
(3)
For we have
Since,
So,
So is increasing in
Now,
Hence, both statements are true.
Q 2
:
The interval in which the function is strictly increasing is [2024]
(1)
So,
For to be strictly increasing, we have
Q 3
:
The number of critical points of the function is [2024]
1
2
3
0
(2)
Given,
For critical points, or is non-existence.
Critical points are i.e., 2 in number.
Q 4
:
For the function between the following two statements [2024]
(S1) for only one value of in
(S2) is decreasing in and increasing in
Only (S2) is correct.
Both (S1) and (S2) are incorrect.
Only (S1) is correct.
Both (S1) and (S2) are correct.
(3)
We have,
For
Now,
So, is strictly decreasing in .
So, has one solution in
(S1) is correct but (S2) is incorrect.
Q 5
:
[2024]
20
18
0
24
(2)
...(i)
Differentiating (i) w.r.t. we get
When is decreasing,
Therefore, So,
Q 6
:
Consider the function defined by
Consider the statements
(I) The curve intersects the -axis exactly at one point.
(II) The curve intersects the -axis at
Then
Both (I) and (II) are incorrect.
Only (I) is correct.
Both (I) and (II) are correct.
Only (II) is correct.
(3)
Q 7
:
The function [2024]
decreases in and increases in
decreases in and increases in
increases in
decreases in
(4)
Q 8
:
Let be strictly increasing function such that Then, the value of is equal to [2024]
4
0
7/5
1
(2)
Q 9
:
Let the set of all values of for which does not have any critical point, be the interval Then is equal to ______ . [2024]
(252)
[ has no critical points]
Q 10
:
If and then is strictly increasing in [2024]
(4)
...(i)
Replace x by , we get:
...(ii)
and , we get
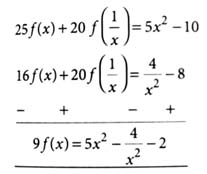
As is strictly increasing when so