sets relations and functions jee mains questions | JEE Main Mathematics Sets Relations And Functions

Q 41 :
If $f (x) = \frac{4 x + 3}{6 x - 4}, x \neq \frac{2}{3}$ and $(f o f) (x) = g (x)$ , where $g : R - {\frac{2}{3}} \to R - {\frac{2}{3}},$ then $(g o g o g) (4)$ is equal to [2024]

$\frac{19}{20}$
$- \frac{19}{20}$
$- 4$
$4$

1

2

3

4

(4)

Here, $f (x) = \frac{4 x + 3}{6 x - 4}$

$f [f (x)] = \frac{4 f (x) + 3}{6 f (x) - 4} = \frac{4 (\frac{4 x + 3}{6 x - 4}) + 3}{6 (\frac{4 x + 3}{6 x - 4}) - 4}$

$= \frac{16 x + 12 + 18 x - 12}{6 x - 4} = \frac{34 x}{34} = x$

$∴$ $f [f (x)] = x \Rightarrow g (x) = x$

Now, $(g o g o g) (4) = g o g [g (4)] = g o g (4) = g (4) = 4$

Q 42 :
Consider the function $f : R \to R$ defined by $f (x) = \frac{2 x}{\sqrt{1 + 9 x^{2}}} .$ If the composition of $\underset{10 times}{f, \underset{⏟}{(f o f o f o . . . o f)}} (x)$ $= \frac{2^{10} x}{\sqrt{1 + 9 α x^{2}}},$ then the value of $\sqrt{3 α + 1}$ is equal to _________ . [2024]

0%

(1024)

We have, $f (x) = \frac{2 x}{\sqrt{1 + 9 x^{2}}}$

$∴$ $(f o f) (x) = \frac{2 f (x)}{\sqrt{1 + 9 (f {(x))}^{2}}} = \frac{\frac{4 x}{\sqrt{1 + 9 x^{2}}}}{\sqrt{1 + 9 \times \frac{4 x^{2}}{1 + 9 x^{2}}}} = \frac{4 x}{\sqrt{1 + 45 x^{2}}} = \frac{2^{2} x}{\sqrt{1 + 5 \times 9 x^{2}}}$

$(f o f o f) (x) = \frac{4 \times \frac{2 x}{\sqrt{1 + 9 x^{2}}}}{\sqrt{1 + 45 \times \frac{4 x^{2}}{1 + 9 x^{2}}}} = \frac{2^{3} x}{\sqrt{1 + 21 \times 9 x^{2}}}$

$(f o f o f o f) (x) = \frac{2^{4} x}{\sqrt{1 \times 85 \times 9 x^{2}}}$

$∴$ $\underset{n times}{\underset{⏟}{(f o f o f o . . . . . o f)}} (x)$ $= \frac{2^{n} x}{\sqrt{1 + 9 (\frac{4^{n} - 1}{3}) x^{2}}}$

$∴$ $\underset{10 times}{\underset{⏟}{(f o f o f o . . . . . o f)}} (x)$ $= \frac{2^{10} x}{\sqrt{1 + 9 (\frac{4^{10} - 1}{3}) x^{2}}} = \frac{2^{10} x}{\sqrt{1 + 9 α x^{2}}}$

( $∵$ Given)

On comparing, we get

$α = \frac{4^{10} - 1}{3} \Rightarrow 3 α + 1 = 4^{10}$

$\Rightarrow \sqrt{3 α + 1} = \sqrt{4^{10}} = 4^{5} = 1024 .$

Q 43 :
If a function $f$ satisfies $f (m + n) = f (m) + f (n)$ for all $m,$ $n \in N$ and $f (1) = 1$ , then the largest natural number $λ$ such that $\sum_{k = 1}^{2022} f (λ + k) \leq {(2022)}^{2}$ is equal to ___________ . [2024]

0%

(1010)

We have, $f (m + n) = f (m) + f (n)$

So, $f (x) = k x$

$∵$ $f (1) = 1 \Rightarrow k = 1$

Hence, $f (x) = x$

Now, $\sum_{k = 1}^{2022} f (λ + k) = \sum_{k = 1}^{2022} (λ + k)$

$= \underset{2022}{\underset{⏟}{λ + λ + . . . + λ}}$ $+ (1 + 2 + . . . . + 2022)$

$= 2022 λ + \frac{2022 \times 2023}{2} \leq {(2022)}^{2}$ (Given)

$\Rightarrow λ \leq \frac{2021}{2}$

So, largest $λ = 1010$

Q 44 :
Let $A = {(x, y) : 2 x + 3 y = 23, x, y \in N}$ and $B = {x : (x, y) \in A}$ . Then the number of one-one functions from A to B is equal to ________ . [2024]

0%

(24)

We have, $A = {(x, y) : 2 x + 3 y = 23, x, y \in N}$

$B = {x : (x, y) \in A}$

$∴ A = {(1, 7), (4, 5), (7, 3), (10, 1)}$

and $B = {1, 4, 7, 10}$

Total number of one-one functions from A to B = 4! = 24

Q 45 :
Let A = {1, 2, 3, ..., 7} and let P(A) denote the power set of A. If the number of functions $f : A \to P (A)$ such that $a \in f (a)$ , $\forall$ $a \in A$ is $m^{n}$ , $m$ and $n \in N$ and $m$ is least, then $m + n$ is equal to _____. [2024]

0%

(44)

Given, $f : A \to P (A) \Rightarrow a \in f (a)$

It means $' a'$ will connect with subset which contain element $a .$

Total options for 1 will be $2^{6}$ ( $∵$ $2^{6}$ subsets contains 1)

Similarly, for every other element

Now, number of functions from A to P(A) = ${(2^{6})}^{7} = 2^{42}$

i.e., $m + n = 2 + 42 = 44$

Q 46 :
Let $f, g : R \to R$ be defined as: [2024]

$f (x) = | x - 1 |$ and $g (x) =$ ${\begin{matrix} e^{x}, & x \geq 0 \\ x + 1, & x \leq 0 \end{matrix} .$

Then the function $f (g (x))$ is

onto but not one-one.
neither one-one nor onto.
both one-one and onto.
one-one but not onto.

1

2

3

4

(2)

$f (g (x)) = | g (x) - 1 |$

$=$ ${\begin{matrix} | e^{x} - 1 |, & x \geq 0 \\ | x + 1 - 1 |, & x \leq 0 \end{matrix}$

$=$ ${\begin{matrix} e^{x} - 1, & x \geq 0 \\ - x, & x \leq 0 \end{matrix}$

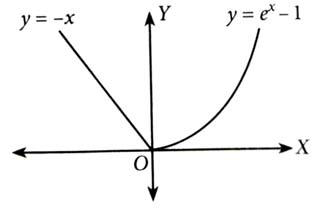
$f (g (x))$ is neither one-one nor onto as negative numbers have no pre-image.

Q 47 :
Let $f : R \to R$ and $g : R \to R$ be defined as:

$f (x)$ $= {\begin{matrix} \log_{e} x, & x > 0 \\ e^{- x}, & x \leq 0 \end{matrix}$ and $g (x)$ $= {\begin{matrix} x, & x \geq 0 \\ e^{x}, & x < 0 \end{matrix} .$

Then, $g o f : R \to R$ is [2024]

neither one-one nor onto
onto but not one-one
one-one but not onto
both one-one and onto

1

2

3

4

(1)

$g (f (x))$ $=$ ${\begin{matrix} f (x), & f (x) \geq 0 \\ e^{f (x)}, & f (x) < 0 \end{matrix}$

$=$ ${\begin{matrix} \log_{e} x, & x \geq 1 \\ e^{- x}, & x \leq 0 \\ e^{\log_{e} x} = x, & 0 < x < 1 \end{matrix}$

$g o f (x) =$ ${\begin{matrix} e^{- x}, & x \leq 0 \\ x, & 0 < x < 1 \\ \log_{e} x, & x \geq 1 \end{matrix}$

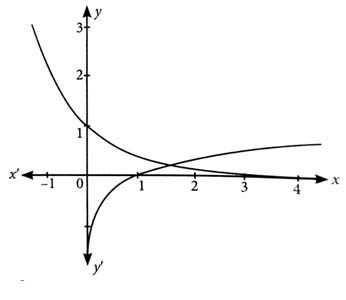
Now, range of $g o f = [0, \infty) \neq R$

Hence, not one-one and not onto.

Q 48 :
If the function $f : (- \infty, - 1] \to (a, b]$ defined by $f (x) = e^{x^{3} - 3 x + 1}$ is one-one and onto, then the distance of the point $P (2 b + 4, a + 2)$ from the line $x + e^{- 3} y = 4$ is : [2024]

$2 \sqrt{1 + e^{6}}$
$4 \sqrt{1 + e^{6}}$
$3 \sqrt{1 + e^{6}}$
$\sqrt{1 + e^{6}}$

1

2

3

4

(1)

Given $f (x) = e^{x^{3} - 3 x + 1}$

$∴$ $f' (x) = e^{x^{3} - 3 x + 1} [3 (x - 1) (x + 1)] \geq 0$

As, $e^{x^{3} - 3 x + 1}$ is always positive.

$∴$ $3 (x - 1) (x + 1) \geq 0$

$\Rightarrow x \in (- \infty, - 1] \cup [1, \infty)$

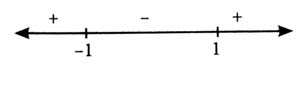
For onto function, Range = Co-domain

$∴$ $a = f (- \infty) = e^{- \infty} = 0$

and $b = f (- 1) = e^{- 1 + 3 + 1} = e^{3}$

$∴$ $P (2 b + 4, a + 2) = P (2 e^{3} + 4, 2)$

Now, distance of the point $P (2 e^{3} + 4, 2)$ from the line $x + e^{- 3} y - 4 = 0$

$= \frac{2 e^{3} + 4 + 2 e^{- 3} - 4}{\sqrt{1 + e^{- 6}}} = \frac{2 (e^{3} + e^{- 3})}{\sqrt{1 + e^{- 6}}} = 2 (\frac{e^{6} + 1}{e^{3}}) \times \frac{1}{\sqrt{1 + e^{6}}} \times e^{3}$

$= 2 \sqrt{1 + e^{6}}$

Q 49 :
If the domain of the function

$f (x) = \frac{1}{\sqrt{10 + 3 x - x^{2}}} + \frac{1}{\sqrt{x + | x |}}$ is (a, b), then

${(1 + a)}^{2} + b^{2}$ is equal to: [2025]

29
26
30
25

1

2

3

4

(2)

We have, $f (x) = \frac{1}{\sqrt{10 + 3 x - x^{2}}} + \frac{1}{\sqrt{x + | x |}}$

For f(x) to be defined, we must have $10 + 3 x - x^{2} > 0$

$\Rightarrow x^{2} - 3 x - 10 < 0 \Rightarrow (x - 5) (x + 2) < 0 \Rightarrow - 2 < x < 5$

Also, x + |x| > 0

Now, if x > 0, then x + |x| > 0

If x < 0, then |x| = –x $\Rightarrow$ x + |x| = x – x = 0

$∴$ The domain of $\frac{1}{\sqrt{x + | x |}}$ is x > 0

$∴$ Domain of f(x) is 0 < x < 5 i.e., (0, 5)

$∴$ a = 0 and b = 5

$\Rightarrow {(1 + a)}^{2} + b^{2} = 1^{2} + 5^{2} = 26$ .

Q 50 :
If the domain of the function

$f (x) = \log_{e} (\frac{2 x - 3}{5 + 4 x}) + \sin^{- 1} (\frac{4 + 3 x}{2 - x}) is [α, β), then α^{2} + 4 β$

is equal to [2025]

7
5
3
4

1

2

3

4

(4)

We have, $f (x) = \log_{e} (\frac{2 x - 3}{5 + 4 x}) + \sin^{- 1} (\frac{4 + 3 x}{2 - x})$

For f(x) to be defined we have,

$\frac{2 x - 3}{5 + 4 x} > 0 and | \frac{4 + 3 x}{2 - x} | \leq 1$

Now, $\frac{2 x - 3}{5 + 4 x} > 0$

Case I : 2x – 3 > 0 and 5 + 4x > 0

$\Rightarrow$ x > 3/2 and x > – 5/4

$\Rightarrow x \in (3 / 2, \infty)$ ... (i)

Case II : 2x – 3 < 0 and 5 + 4x < 0

$\Rightarrow$ x < 3/2 and x < – 5/4

$\Rightarrow x \in (- \infty, - 5 / 4)$ ... (ii)

From (i) and (ii), we get

$x \in (- \infty, - \frac{5}{4}) \cup (\frac{3}{2}, \infty)$ ... (iii)

Also, $| \frac{4 + 3 x}{2 - x} | \leq 1$

$\Rightarrow - 1 \leq \frac{4 + 3 x}{2 - x} \leq 1 \Rightarrow - 1 \leq \frac{4 + 3 x}{2 - x} and \frac{4 + 3 x}{2 - x} \leq 1$

$\Rightarrow 0 \leq \frac{4 + 3 x}{2 - x} + 1 and \frac{4 + 3 x}{2 - x} - 1 \leq 0$

$\Rightarrow 0 \leq \frac{6 + 2 x}{2 - x} and \frac{2 + 4 x}{2 - x} \leq 0$

$\Rightarrow - 3 \leq x and x \leq - \frac{1}{2}, x \neq 2$

$\Rightarrow x \in [- 3, - \frac{1}{2}]$ ... (iv)

From (iii) and (iv), we get

$x \in [- 3, - \frac{5}{4})$

$∴ α = - 3 and β = - \frac{5}{4}$

Thus, $α^{2} + 4 β = 9 - 5 = 4 .$ .

Topic Question Set

Q 41 :
If $f (x) = \frac{4 x + 3}{6 x - 4}, x \neq \frac{2}{3}$ and $(f o f) (x) = g (x)$ , where $g : R - {\frac{2}{3}} \to R - {\frac{2}{3}},$ then $(g o g o g) (4)$ is equal to [2024]

Q 42 :
Consider the function $f : R \to R$ defined by $f (x) = \frac{2 x}{\sqrt{1 + 9 x^{2}}} .$ If the composition of $\underset{10 times}{f, \underset{⏟}{(f o f o f o . . . o f)}} (x)$ $= \frac{2^{10} x}{\sqrt{1 + 9 α x^{2}}},$ then the value of $\sqrt{3 α + 1}$ is equal to _________ . [2024]

0%

Q 43 :
If a function $f$ satisfies $f (m + n) = f (m) + f (n)$ for all $m,$ $n \in N$ and $f (1) = 1$ , then the largest natural number $λ$ such that $\sum_{k = 1}^{2022} f (λ + k) \leq {(2022)}^{2}$ is equal to ___________ . [2024]

0%

Q 44 :
Let $A = {(x, y) : 2 x + 3 y = 23, x, y \in N}$ and $B = {x : (x, y) \in A}$ . Then the number of one-one functions from A to B is equal to ________ . [2024]

0%

Q 45 :
Let A = {1, 2, 3, ..., 7} and let P(A) denote the power set of A. If the number of functions $f : A \to P (A)$ such that $a \in f (a)$ , $\forall$ $a \in A$ is $m^{n}$ , $m$ and $n \in N$ and $m$ is least, then $m + n$ is equal to _____. [2024]

0%

Q 46 :
Let $f, g : R \to R$ be defined as: [2024]

$f (x) = | x - 1 |$ and $g (x) =$ ${\begin{matrix} e^{x}, & x \geq 0 \\ x + 1, & x \leq 0 \end{matrix} .$

Then the function $f (g (x))$ is

Q 47 :
Let $f : R \to R$ and $g : R \to R$ be defined as:

$f (x)$ $= {\begin{matrix} \log_{e} x, & x > 0 \\ e^{- x}, & x \leq 0 \end{matrix}$ and $g (x)$ $= {\begin{matrix} x, & x \geq 0 \\ e^{x}, & x < 0 \end{matrix} .$

Then, $g o f : R \to R$ is [2024]

Q 48 :
If the function $f : (- \infty, - 1] \to (a, b]$ defined by $f (x) = e^{x^{3} - 3 x + 1}$ is one-one and onto, then the distance of the point $P (2 b + 4, a + 2)$ from the line $x + e^{- 3} y = 4$ is : [2024]

Q 49 :
If the domain of the function

$f (x) = \frac{1}{\sqrt{10 + 3 x - x^{2}}} + \frac{1}{\sqrt{x + | x |}}$ is (a, b), then

${(1 + a)}^{2} + b^{2}$ is equal to: [2025]

Q 50 :
If the domain of the function

$f (x) = \log_{e} (\frac{2 x - 3}{5 + 4 x}) + \sin^{- 1} (\frac{4 + 3 x}{2 - x}) is [α, β), then α^{2} + 4 β$

is equal to [2025]

Want Us to Email you About Special Offers & Updates?

Topic Question Set

Q 41 : If f(x)=4x+36x-4, x≠23 and (fof)(x)=g(x), where g:R-{23}→R-{23}, then (gogog)(4) is equal to [2024]

Q 42 : Consider the function f:R→R defined by f(x)=2x1+9x2. If the composition of f,(fofofo...of)⏟10 times (x) =210x1+9αx2, then the value of 3α+1 is equal to _________ . [2024]

0%

Q 43 : If a function f satisfies f(m+n)=f(m)+f(n) for all m, n∈N and f(1)=1, then the largest natural number λ such that ∑k=12022f(λ+k)≤(2022)2 is equal to ___________ . [2024]

0%

Q 44 : Let A={(x,y):2x+3y=23,x,y∈N} and B={x:(x,y)∈A}. Then the number of one-one functions from A to B is equal to ________ . [2024]

0%

Q 45 : Let A = {1, 2, 3, ..., 7} and let P(A) denote the power set of A. If the number of functions f:A→P(A) such that a∈f(a), ∀ a∈A is mn, m and n∈N and m is least, then m+n is equal to _____. [2024]

0%

Q 46 : Let f,g:R→R be defined as: [2024] f(x)=|x-1| and g(x)={ex,x≥0x+1,x≤0. Then the function f(g(x)) is

Q 47 : Let f:R→R and g:R→R be defined as: f(x)={logex,x>0e-x,x≤0 and g(x)={x,x≥0ex,x<0. Then, gof:R→R is [2024]

Q 48 : If the function f:(-∞,-1]→(a,b] defined by f(x)=ex3-3x+1 is one-one and onto, then the distance of the point P(2b+4, a+2) from the line x+e-3y=4 is : [2024]

Q 49 : If the domain of the function f(x)=110+3x–x2+1x+|x| is (a, b), then (1+a)2+b2 is equal to: [2025]

Q 50 : If the domain of the function f(x)=loge(2x–35+4x)+sin–1(4+3x2–x) is [α,β), then α2+4β is equal to [2025]

Want Us to Email you About Special Offers & Updates?

Q 41 :
If $f (x) = \frac{4 x + 3}{6 x - 4}, x \neq \frac{2}{3}$ and $(f o f) (x) = g (x)$ , where $g : R - {\frac{2}{3}} \to R - {\frac{2}{3}},$ then $(g o g o g) (4)$ is equal to [2024]

Q 42 :
Consider the function $f : R \to R$ defined by $f (x) = \frac{2 x}{\sqrt{1 + 9 x^{2}}} .$ If the composition of $\underset{10 times}{f, \underset{⏟}{(f o f o f o . . . o f)}} (x)$ $= \frac{2^{10} x}{\sqrt{1 + 9 α x^{2}}},$ then the value of $\sqrt{3 α + 1}$ is equal to _________ . [2024]

Q 43 :
If a function $f$ satisfies $f (m + n) = f (m) + f (n)$ for all $m,$ $n \in N$ and $f (1) = 1$ , then the largest natural number $λ$ such that $\sum_{k = 1}^{2022} f (λ + k) \leq {(2022)}^{2}$ is equal to ___________ . [2024]

Q 44 :
Let $A = {(x, y) : 2 x + 3 y = 23, x, y \in N}$ and $B = {x : (x, y) \in A}$ . Then the number of one-one functions from A to B is equal to ________ . [2024]

Q 45 :
Let A = {1, 2, 3, ..., 7} and let P(A) denote the power set of A. If the number of functions $f : A \to P (A)$ such that $a \in f (a)$ , $\forall$ $a \in A$ is $m^{n}$ , $m$ and $n \in N$ and $m$ is least, then $m + n$ is equal to _____. [2024]

Q 46 :
Let $f, g : R \to R$ be defined as: [2024]

$f (x) = | x - 1 |$ and $g (x) =$ ${\begin{matrix} e^{x}, & x \geq 0 \\ x + 1, & x \leq 0 \end{matrix} .$

Then the function $f (g (x))$ is

Q 47 :
Let $f : R \to R$ and $g : R \to R$ be defined as:

$f (x)$ $= {\begin{matrix} \log_{e} x, & x > 0 \\ e^{- x}, & x \leq 0 \end{matrix}$ and $g (x)$ $= {\begin{matrix} x, & x \geq 0 \\ e^{x}, & x < 0 \end{matrix} .$

Then, $g o f : R \to R$ is [2024]

Q 48 :
If the function $f : (- \infty, - 1] \to (a, b]$ defined by $f (x) = e^{x^{3} - 3 x + 1}$ is one-one and onto, then the distance of the point $P (2 b + 4, a + 2)$ from the line $x + e^{- 3} y = 4$ is : [2024]

Q 49 :
If the domain of the function

$f (x) = \frac{1}{\sqrt{10 + 3 x - x^{2}}} + \frac{1}{\sqrt{x + | x |}}$ is (a, b), then

${(1 + a)}^{2} + b^{2}$ is equal to: [2025]

Q 50 :
If the domain of the function

$f (x) = \log_{e} (\frac{2 x - 3}{5 + 4 x}) + \sin^{- 1} (\frac{4 + 3 x}{2 - x}) is [α, β), then α^{2} + 4 β$

is equal to [2025]