Let A = {1, 2, 3, 4, 5, 6, 7}. Then the relation is [2023]
an equivalence relation
reflexive but neither symmetric nor transitive
transitive but neither symmetric nor reflexive
symmetric but neither reflexive nor transitive

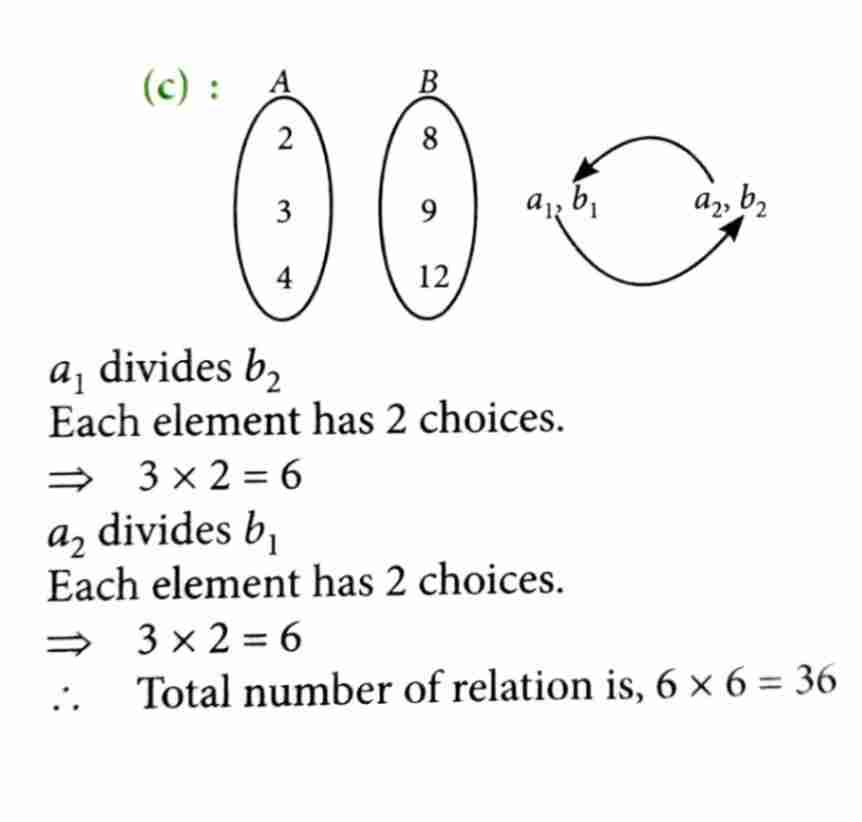
Let A = {2, 3, 4} and B = {8, 9, 12}. Then the number of elements in the relation
divides and divides is [2023]
24
12
36
18
Let A = {1, 3, 4, 6, 9} and B = {2, 4, 5, 8, 10}. Let R be a relation defined on A x B such that and Then the number of elements in the set R is [2023]
52
180
26
160

Let R be a relation on R, given by
R = is an irrational number
Then R is [2023]
reflexive and symmetric but not transitive
reflexive and transitive but not symmetric
reflexive but neither symmetric nor transitive
an equivalence relation

Let P(S) denote the power set of S = {1, 2, 3, ...., 10}. Define the relations and on P(S) as if and if . Then [2023]
both and are not equivalence relations
only is an equivalence relation
only is an equivalence relation
both and are equivalence relations
The relation is [2023]
reflexive but not symmetric
transitive but not reflexive
symmetric but not transitive
neither symmetric nor transitive
Enter Answer here
Let R be a relation defined on as if is a multiple of 5, . [2023]
symmetric but not transitive
not reflexive
an equivalence relation
transitive but not symmetric

The minimum number of elements that must be added to the relation R = {(a, b), (b, c)} on the set {a, b, c} so that it becomes symmetric and transitive is [2023]
3
7
4
5

Let R be a relation on N x N defined by (a, b) R(c, d) if and only if . Then R is [2023]
transitive but neither reflexive nor symmetric
symmetric but neither reflexive nor transitive
symmetric and transitive but not reflexive
reflexive and symmetric but not transitive

Among the relations
and
[2023]
S is transitive but T is not
both S and T are symmetric
neither S nor T is transitive
T is symmetric but S is not
