Differential Calculus jee mains questions | JEE Main Maths Quadratic Equations Previous Year Question

Q 41 :

Let m and n be number of points at which the function $f (x) = \max {x, x^{3}, x^{5}, . . ., x^{21}}, x \in R$ , is not differentiable and not continuous, respectively, Then m + n is equal to __________. [2025]

0%

(3)

Here, $f (x)$ $= {\begin{matrix} x, & x < - 1 \\ x^{21}, & - 1 \leq x < 0 \\ x, & 0 \leq x < 1 \\ x^{21}, & x \geq 1 \end{matrix}$ is continuous everywhere.

Then, n = 0

$\Rightarrow f' (x)$ $= {\begin{matrix} 1, & x < - 1 \\ 21 x^{20}, & - 1 \leq x < 0 \\ 1, & 0 \leq x < 1 \\ 21 x^{20}, & x \geq 1 \end{matrix}$ is not differentiable at

$x = - 1, 0, 1 \Rightarrow m = 3$

So, m + n = 3.

Q 42 :

The number of points of discontinuity of the function $f (x)$ $= [\frac{x^{2}}{2}] - [\sqrt{x}], x \in [0, 4]$ , where $[\cdot]$ denotes the greatest integer function, is __________. [2025]

0%

(8)

Values of x, where $[\frac{x^{2}}{2}]$ may be discontinuous on $x \in [0, 4]$ are $\sqrt{2}, 2, \sqrt{6}, 2 \sqrt{2}, \sqrt{10}, 2 \sqrt{3}, \sqrt{14}, 4$

And for $[\sqrt{x}]$ , values of x are = 1, 4

On checking for continuity at these points, we get f(x) is discontinuous at $x = 1, \sqrt{2}, 2, \sqrt{6}, 2 \sqrt{2}, \sqrt{10}, 2 \sqrt{3}, \sqrt{14}$ and continuous at x = 4.

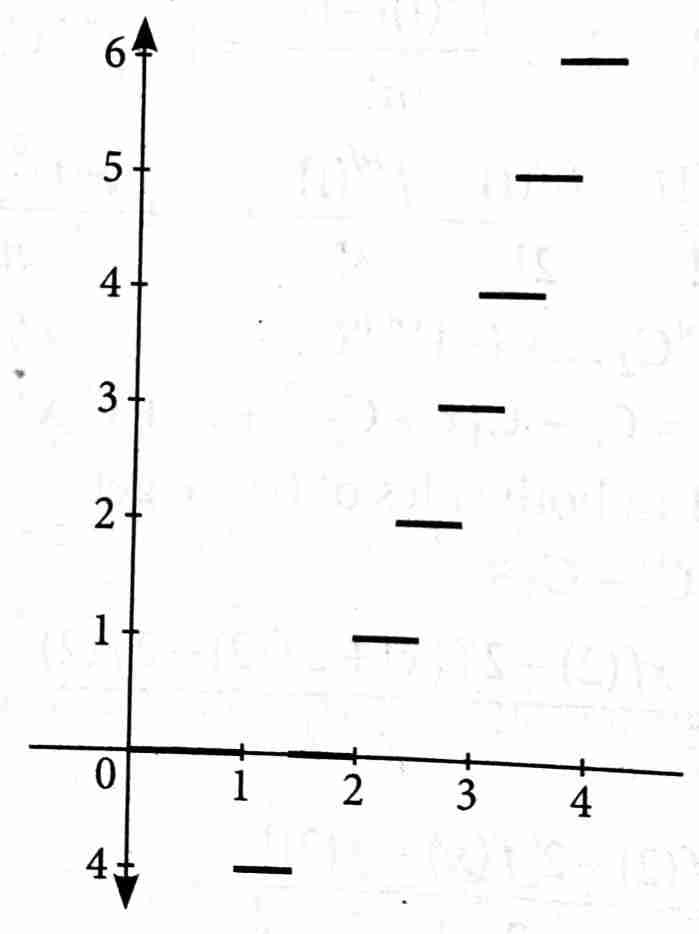
Hence, f(x) is discontinuous for 8 values of $x \in [0, 4]$ .

Q 43 :

If the function $f (x) = \frac{\tan (\tan x) - \sin (\sin x)}{\tan x - \sin x}$ is continuous at x = 0, then f(0) is equal to ________. [2025]

0%

(2)

$f (0) = \lim_{x \to 0} \frac{\tan (\tan x) - \sin (\sin x) - \tan x + \tan x - \sin x + \sin x}{\tan x - \sin x}$

$= \lim_{x \to 0} \frac{\frac{\tan (\tan x) - \tan x}{\tan^{3} x} \times \frac{\tan^{3} x}{x^{3}} + \frac{\tan x - \sin x}{x^{3}} + \frac{\sin x - \sin (\sin x)}{\sin^{3} x} \times \frac{\sin^{3} x}{x^{3}}}{\frac{\tan x - \sin x}{x^{3}}}$

$= 1 + \frac{(\frac{1}{3} + \frac{1}{6})}{(\frac{1}{3} + \frac{1}{6})} = 2$ . [From L'Hospital's Rule]

Q 44 :

Let $f (x)$ $= {\begin{matrix} 3 x, & x < 0 \\ \min {1 + x + [x], x + 2 [x]}, & 0 \leq x \leq 2 \\ 5, & x > 2 \end{matrix}$ , where $[\cdot]$ denotes greatest integer function. If $α$ and $β$ are the number of points, where f is not continuous and is not differentiable, respectively, then $α + β$ equals __________. [2025]

0%

(5)

$f (x)$ $= {\begin{matrix} 3 x, & x < 0 \\ \min {1 + x + [x], x + 2 [x]}, & 0 \leq x \leq 2 \\ 5, & x > 2 \end{matrix}$

$\Rightarrow$ $f (x)$ $= {\begin{matrix} 3 x, & x < 0 \\ x, & 0 \leq x < 1 \\ x + 2, & 1 \leq x < 2 \\ 5, & x > 2 \end{matrix}$

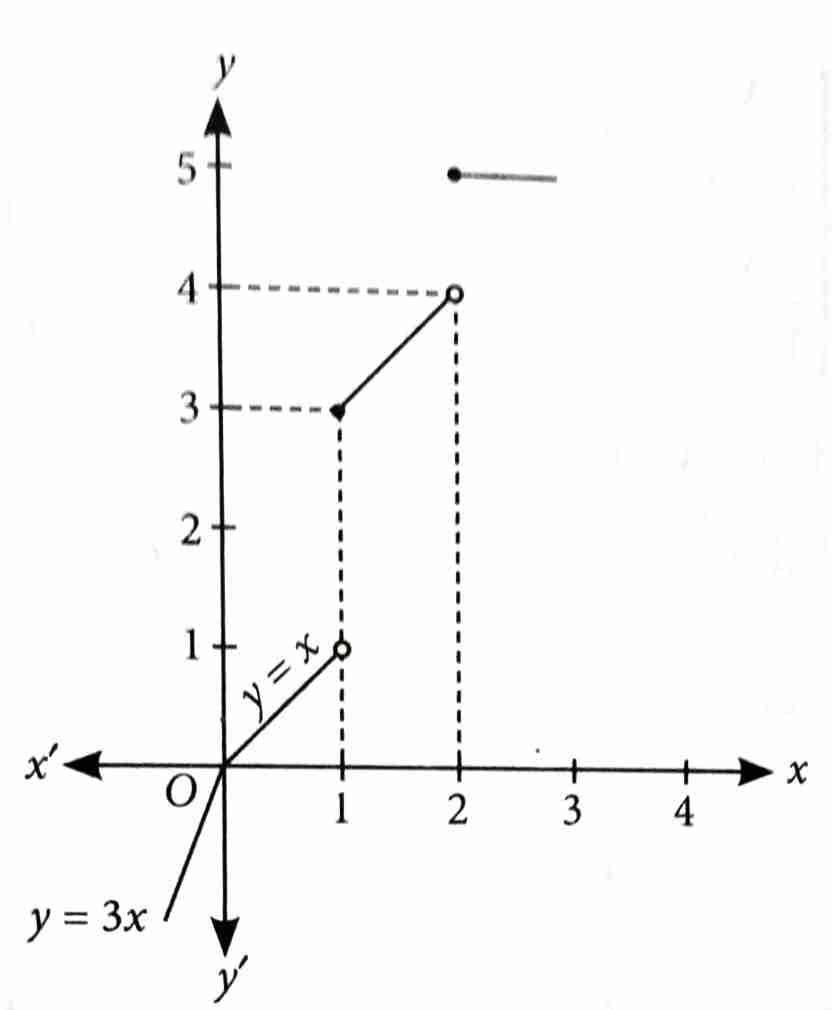
$∴$ By graph, we have f(x) is not continuous at $x \in {1, 2} \Rightarrow α = 2$

f(x) is not differentiable at $x \in {0, 1, 2} \Rightarrow β = 3$

$∴ α + β = 5$ .

Q 45 :

$If 2 x^{y} + 3 y^{x} = 20, then \frac{d y}{d x} at (2, 2) is equal to$ [2023]

$- (\frac{3 + \log_{e} 8}{2 + \log_{e} 4})$
$- (\frac{3 + \log_{e} 16}{4 + \log_{e} 8})$
$- (\frac{3 + \log_{e} 4}{2 + \log_{e} 8})$
$- (\frac{2 + \log_{e} 8}{3 + \log_{e} 4})$

1

2

3

4

(4)

Q 46 :

$Let f (x) = \frac{\sin x + \cos x - \sqrt{2}}{\sin x - \cos x}, x \in [0, π] - {\frac{π}{4}} .$ Then $f (\frac{7 π}{12}) f'' (\frac{7 π}{12})$ is equal to [2023]

$\frac{- 1}{3 \sqrt{3}}$
$\frac{2}{9}$
$\frac{2}{3 \sqrt{3}}$
$\frac{- 2}{3}$

1

2

3

4

(2)

$Given f (x) = \frac{\sin x + \cos x - \sqrt{2}}{\sin x - \cos x}$

$\Rightarrow$ $f (x) = \frac{\frac{1}{\sqrt{2}} \sin x + \frac{1}{\sqrt{2}} \cos x - 1}{\frac{1}{\sqrt{2}} \sin x - \frac{1}{\sqrt{2}} \cos x}$

$= \frac{\sin (\frac{π}{4}) \cdot \sin x + \cos (\frac{π}{4}) \cdot \cos x - 1}{\cos \frac{π}{4} \cdot \sin x - \sin \frac{π}{4} \cdot \cos x}$

$\Rightarrow f (x) = \frac{\cos (x - \frac{π}{4}) - 1}{\sin (x - \frac{π}{4})} = \frac{- 2 \sin^{2} (\frac{x}{2} - \frac{π}{8})}{2 \sin (\frac{x}{2} - \frac{π}{8}) \cdot \cos (\frac{x}{2} - \frac{π}{8})}$

$\Rightarrow f (x) = - \tan (\frac{x}{2} - \frac{π}{8}) \Rightarrow f' (x) = - \frac{1}{2} \sec^{2} (\frac{x}{2} - \frac{π}{8})$

$and f'' (x) = - \frac{1}{2} \times 2 \sec (\frac{x}{2} - \frac{π}{8}) \cdot \sec (\frac{x}{2} - \frac{π}{8}) \cdot \tan (\frac{x}{2} - \frac{π}{8}) \times \frac{1}{2}$

$\Rightarrow f'' (x) = - \frac{1}{2} \sec^{2} (\frac{x}{2} - \frac{π}{8}) \cdot \tan (\frac{x}{2} - \frac{π}{8})$

$∴$ $f'' (\frac{7 π}{12}) = - \frac{1}{2} \sec^{2} (\frac{7 π}{24} - \frac{π}{8}) \cdot \tan (\frac{7 π}{24} - \frac{π}{8})$

$= - \frac{1}{2} \sec^{2} (\frac{π}{6}) \cdot \tan (\frac{π}{6}) = - \frac{1}{2} \times \frac{4}{3} \cdot \frac{1}{\sqrt{3}} = - \frac{2}{3 \sqrt{3}}$

$Also, f (\frac{7 π}{12}) = - \tan (\frac{π}{6}) = - \frac{1}{\sqrt{3}}$

$∴$ $f (\frac{7 π}{12}) \cdot f'' (\frac{7 π}{12}) = \frac{- 2}{3 \sqrt{3}} \times \frac{- 1}{\sqrt{3}} = \frac{2}{9}$

Q 47 :

Let $f (x) = [x^{2} - x] +$ $| - x + [x] |$ , where $x \in ℝ$ and $[t]$ denotes the greatest integer less than or equal to t. Then, $f$ is: [2023]

continuous at $x = 0$ , but not continuous at $x = 1$
continuous at $x = 0$ and $x = 1$
not continuous at $x = 0$ and $x = 1$
continuous at $x = 1$ , but not continuous at $x = 0$

1

2

3

4

(4)

We have, $f (x) = [x^{2} - x] +$ $| - x + [x] |$

$= [x (x - 1)] +$ $| - x + x - {x} |$

$\Rightarrow f (x) = [x (x - 1)] + {x}$

$f (0^{+}) = - 1 + 0 = - 1$	$R.H.L. = f (1^{+}) = 0 + 0 = 0$
$f (0) = 0$	$f (1) = 0$
	$L.H.L. = f (1^{-}) = - 1 + 1 = 0$

$∴$ $f (x) is continuous at x = 1, and discontinuous at x = 0 .$

Q 48 :

$Let f and g be two functions defined by$ $f (x) =$ ${\begin{matrix} x + 1, & x < 0 \\ | x - 1 |, & x \geq 0 \end{matrix}$ and $g (x) =$ ${\begin{matrix} x + 1, & x < 0 \\ 1, & x \geq 0 \end{matrix}$ Then $(g o f) (x)$ is [2023]

continuous everywhere but not differentiable exactly at one point
not continuous at $x = - 1$
continuous everywhere but not differentiable at $x = 1$
differentiable everywhere

1

2

3

4

(1)

We have,

$f (x) =$ ${\begin{matrix} x + 1, & x < 0 \\ | x - 1 |, & x \geq 0 \end{matrix}$ and $g (x) =$ ${\begin{matrix} x + 1, & x < 0 \\ 1, & x \geq 0 \end{matrix}$

$f (x) =$ ${\begin{matrix} x + 1, & x < 0 \\ x - 1, & x \geq 1 \\ 1 - x, & 0 \leq x < 1 \end{matrix}$ $∴$ $(g o f) (x) =$ ${\begin{matrix} x + 2, & x < - 1 \\ 1, & x \geq - 1 \end{matrix}$

$Hence, (g o f) (x) is not differentiable at x = - 1, but it is continuous everywhere.$

Q 49 :

For the differentiable function $f : ℝ - {0} \to ℝ, let 3 f (x) + 2 f (\frac{1}{x}) = \frac{1}{x} - 10, then$ $| f (3) + f' (\frac{1}{4}) |$ is equal to [2023]

13
7
$\frac{33}{5}$
$\frac{29}{5}$

1

2

3

4

(1)

Given, $3 f (x) + 2 f (\frac{1}{x}) = \frac{1}{x} - 10 ...(i)$

Put $x = \frac{1}{x}$ in (i), we get $3 f (\frac{1}{x}) + 2 f (x) = x - 10 ...(ii)$

Multiply (i) by 3 and (ii) by 2, then (i) − (ii):

$5 f (x) = \frac{3}{x} - 2 x - 10 \Rightarrow f (x) = \frac{1}{5} (\frac{3}{x} - 2 x - 10)$

Differentiate it w.r.t. $x,$ $f' (x) = \frac{1}{5} (\frac{- 3}{x^{2}} - 2)$

$∴$ $| f (3) + f' (\frac{1}{4}) |$ $=$ $| \frac{1}{5} (\frac{3}{3} - 2 (3) - 10) + \frac{1}{5} (- 48 - 2) |$

$=$ $| \frac{1}{5} (1 - 6 - 10 - 50) |$ $=$ $| \frac{1}{5} (- 65) |$ $= 13$

Q 50 :

Let $[x]$ denote the greatest integer function and $f (x) = \max {1 + x + [x], 2 + x, x + 2 [x]}, 0 \leq x \leq 2$ . Let $m$ be the number of points in $[0, 2]$ where $f$ is not continuous and $n$ be the number of points in (0, 2) where $f$ is not differentiable. Then ${(m + n)}^{2} + 2$ is equal to [2023]

2
3
6
11

1

2

3

4

(2)

In [0,1]

$f (x) = \max {1 + x, 2 + x, x} = 2 + x$

In (1, 2)

$f (x) = \max {1 + x + 1, 2 + x, x + 2} = 2 + x$

At $x$ = 2

$f (x) = \max {1 + x + 2, 2 + x, x + (2 \times 2)}$

$= \max {x + 3, x + 2, x + 4}$

$= x + 4$

In [0, 2], $f (x)$ is not continuous at $x$ = 2

In (0, 2), $f (x)$ is not differentiable function.

$∴$ $m = 1, n = 0$

$So, {(m + n)}^{2} + 2 = {(1 + 0)}^{2} + 2 = 1 + 2 = 3$

Topic Question Set

Q 41 :

Let m and n be number of points at which the function $f (x) = \max {x, x^{3}, x^{5}, . . ., x^{21}}, x \in R$ , is not differentiable and not continuous, respectively, Then m + n is equal to __________. [2025]

0%

Q 42 :

The number of points of discontinuity of the function $f (x)$ $= [\frac{x^{2}}{2}] - [\sqrt{x}], x \in [0, 4]$ , where $[\cdot]$ denotes the greatest integer function, is __________. [2025]

0%

Q 43 :

If the function $f (x) = \frac{\tan (\tan x) - \sin (\sin x)}{\tan x - \sin x}$ is continuous at x = 0, then f(0) is equal to ________. [2025]

0%

0%

Q 45 :

$If 2 x^{y} + 3 y^{x} = 20, then \frac{d y}{d x} at (2, 2) is equal to$ [2023]

(4)

Q 46 :

$Let f (x) = \frac{\sin x + \cos x - \sqrt{2}}{\sin x - \cos x}, x \in [0, π] - {\frac{π}{4}} .$ Then $f (\frac{7 π}{12}) f'' (\frac{7 π}{12})$ is equal to [2023]

Q 47 :

Let $f (x) = [x^{2} - x] +$ $| - x + [x] |$ , where $x \in ℝ$ and $[t]$ denotes the greatest integer less than or equal to t. Then, $f$ is: [2023]

Q 48 :

$Let f and g be two functions defined by$ $f (x) =$ ${\begin{matrix} x + 1, & x < 0 \\ | x - 1 |, & x \geq 0 \end{matrix}$ and $g (x) =$ ${\begin{matrix} x + 1, & x < 0 \\ 1, & x \geq 0 \end{matrix}$ Then $(g o f) (x)$ is [2023]

Q 49 :

For the differentiable function $f : ℝ - {0} \to ℝ, let 3 f (x) + 2 f (\frac{1}{x}) = \frac{1}{x} - 10, then$ $| f (3) + f' (\frac{1}{4}) |$ is equal to [2023]

Want Us to Email you About Special Offers & Updates?