Differential Calculus jee mains questions | JEE Main Maths Quadratic Equations Previous Year Question

Q 31 :
Consider the function $f : (0, \infty) \to R$ defined by $f (x) = e^{- | \log_{e} x |}$ . If $m$ and $n$ be respectively the number of points at which $f$ is not continuous and $f$ is not differentiable, then $m + n$ is [2024]

1
0
2
3

1

2

3

4

(1)

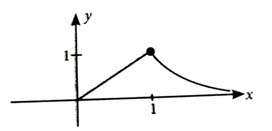
Given, $f (x) = e^{- | \log_{e} x |}$

$\Rightarrow$ $f (x) =$ ${\begin{matrix} 1 / e^{- \log_{e} x}, & 0 < x < 1 \\ 1 / e^{\log_{e} x}, & x \geq 1 \end{matrix} = {\begin{matrix} x, & 0 < x < 1 \\ 1 / x, & x \geq 1 \end{matrix}$

$∴$ $f (x)$ is continuous everywhere for $x > 0$ but not differentiable at $x = 1 .$

Thus, $m = 0, n = 1$

Hence, $m + n = 1$

Q 32 :
Let $f (x) = 2^{x} - x^{2}, x \in R .$ If $m$ and $n$ are respectively the number of points at which the curves $y = f (x)$ and $y = f' (x)$ intersect the $x -$ axis, then the value of $m + n$ is _________. [2024]

0%

(5)

We have, $f (x) = 2^{x} - x^{2}$

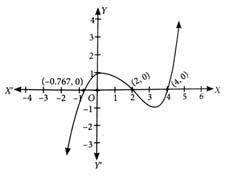
By graph, since $f (x)$ intersects the $x$ -axis at 3 points. So, number of solutions of $f (x) = 3$

$∴$ $m = 3$

Also, $f' (x) = 2^{x} \log 2 - 2 x$

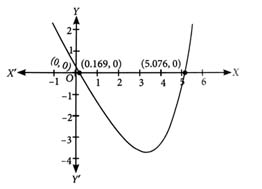
By graph, since $f' (x)$ intersects $x$ -axis at 2 points. So, number of solutions of $f' (x) = 2$

$∴$ $n = 2$

Thus, $m + n = 3 + 2 = 5$

Q 33 :
Let $f : R \to R$ be a twice differentiale function such that (sin x cos y)(f(2x + 2y) – f(2x – 2y)) = (cos x sin y)(f(2x + 2y) + f(2x – 2y)), for all x, y $\in$ R.

If $f' (0) = \frac{1}{2}$ , then the value of $24 f'' (\frac{5 π}{3})$ is : [2025]

–3
–2
3
2

1

2

3

4

(1)

We have,

(sin x cos y)(f(2x + 2y) – f(2x – 2y)) = (cos x sin y)(f(2x + 2y) + f(2x – 2y))

$\Rightarrow$ f(2x + 2y) sin (x – y) = f(2x – 2y) sin (x + y)

$\Rightarrow \frac{f (2 x + 2 y)}{\sin (x + y)} = \frac{f (2 x - 2 y)}{\sin (x - y)}$

Put 2x + 2y = m and 2x – 2y = n, we get

$\frac{f (m)}{\sin (\frac{m}{2})} = \frac{f (n)}{\sin (\frac{n}{2})} = K$

$\Rightarrow f (m) = K \sin (\frac{m}{2}) and f (n) = K \sin (\frac{n}{2})$

$∴$ $f (x) = K \sin (\frac{x}{2}) \Rightarrow f' (x) = \frac{K}{2} \cos (\frac{x}{2})$

Now, $f' (0) = \frac{1}{2} \Rightarrow \frac{1}{2} = \frac{K}{2} \Rightarrow K = 1$

$∴ f' (x) = \frac{1}{2} \cos \frac{x}{2} \Rightarrow f'' (x) = - \frac{1}{4} \sin \frac{x}{2}$

$∴ 24 f'' (\frac{5 π}{3}) = 24 (- \frac{1}{4} \sin (\frac{5 π}{6})) = \frac{- 24}{8} = - 3$ .

Q 34 :
Let $f (x)$ $= {\begin{matrix} {(1 + a x)}^{1 / x}, & x < 0 \\ 1 + b, & x = 0 \\ \frac{{(x + 4)}^{1 / 2} - 2}{{(x + c)}^{1 / 3} - 2} & x > 0 \end{matrix} \begin{matrix} \end{matrix}$ be continuous at x = 0. Then $e^{a} b c$ is equal to : [2025]

48
72
36
64

1

2

3

4

(1)

L.H.L. = $f (0^{-}) = e^{\lim_{x \to 0} \frac{1}{x} \log (1 + a x)} = e^{\lim_{x \to 0} \frac{a}{1 + a x}} = e^{a}$

R.H.L. = $f (0^{+}) = \lim_{x \to 0} \frac{{(x + 4)}^{1 / 2} - 2}{{(x + c)}^{1 / 3} - 2} = \frac{0}{c^{1 / 3} - 2}$

Since, f(x) is continuous at x = 0

$∴$ Right hand limit exists

$\Rightarrow c^{1 / 3} - 2 = 0 \Rightarrow c^{1 / 3} = 2 \Rightarrow c = 8$ ... (i)

Now, $f (0^{+}) = \frac{2 - 2}{2 - 2}$ $(\frac{0}{0} form)$

$= \frac{\frac{1}{2 \sqrt{0 + 4}}}{\frac{1}{3} {(0 + c)}^{- 2 / 3}}$ [Using L'Hospital's Rule]

$= \frac{3}{4} c^{2 / 3} = \frac{3}{4} {(8)}^{2 / 3} = 3$ [From (i)]

Now, $f (0) = f (0^{-}) = f (0^{+})$

$\Rightarrow 1 + b = e^{a} = 3 \Rightarrow b = 2 and e^{a} = 3$

$∴ e^{a} b c = 3 \times 2 \times 8 = 48$ .

Q 35 :
If $y (x)$ $=$ $| \begin{matrix} \sin x & \cos x & \sin x + \cos x + 1 \\ 27 & 28 & 27 \\ 1 & 1 & 1 \end{matrix} |$ $, x \in ℝ$ , then $\frac{d^{2} y}{d x^{2}} + y$ is equal to [2025]

–1
27
1
28

1

2

3

4

(1)

We have,

$y (x)$ $=$ $| \begin{matrix} \sin x & \cos x & \sin x + \cos x + 1 \\ 27 & 28 & 27 \\ 1 & 1 & 1 \end{matrix} |$

$\Rightarrow$ y(x) = sin x (28 – 27) – cos x (27 – 27) + (sin x + cos x + 1)(27 – 28)

y(x) = – cos x – 1

On differentiate w.r.t. x, we get

$\frac{d y}{d x} = \sin x \Rightarrow \frac{d^{2} y}{d x^{2}} = \cos x$

$∴ \frac{d^{2} y}{d x^{2}} + y = \cos x - 1 - \cos x = - 1$ .

Q 36 :
Let $f : R \to R$ be a continuous function satisfying f(0) = 1 and f(2x) – f(x) = x for all x $\in$ R. If $\lim_{n \to \infty} {f (x) - f (\frac{x}{2^{n}})} = G (x)$ , then $\sum_{r = 1}^{10} G (r^{2})$ is equal to [2025]

540
420
385
215

1

2

3

4

(3)

We have, f(2x) – f(x) = x

$\Rightarrow f (x) - f (\frac{x}{2}) = \frac{x}{2}$

$\Rightarrow f (\frac{x}{2}) - f (\frac{x}{4}) = \frac{x}{4}$

$\Rightarrow f (\frac{x}{2^{n - 1}}) - f (\frac{x}{2^{n}}) = \frac{x}{2^{n}}$

On adding all the above statements, we get

$f (2 x) - f (\frac{x}{2^{n}}) = x + \frac{x}{2} + \frac{x}{4} + . . . + \frac{x}{2^{n}}$

$= x {\frac{1 - {(\frac{1}{2})}^{n + 1}}{1 - \frac{1}{2}}} = 2 x [1 - {(\frac{1}{2})}^{n + 1}]$

$\Rightarrow f (x) + x - f (\frac{x}{2^{n}})$

$= 2 x [1 - {(\frac{1}{2})}^{n + 1}]$

$\Rightarrow \lim_{n \to \infty} [f (x) - f (\frac{x}{2^{n}})]$

$= \lim_{n \to \infty} [2 x (1 - {(\frac{1}{2})}^{n + 1}) - x]$

$\Rightarrow G (x) = x \Rightarrow \sum_{r = 1}^{10} r^{2} = 385$ .

Q 37 :
Let f(x) be a real differentiable function such that f(0) = 1 and $f (x + y) = f (x) f' (y) + f' (x) f (y)$ for all x, y $\in$ R. Then $\sum_{n = 1}^{100} \log_{e} f (n)$ is equal to : [2025]

2406
5220
2525
2384

1

2

3

4

(3)

$f (x + y) = f (x) f' (y) + f' (x) f (y)$

When x = 0, y = 0, we have

$f (0) = f (0) f' (0) + f' (0) f (0)$

$\Rightarrow f (0) = 2 f' (0) f (0) \Rightarrow f' (0) = \frac{1}{2}$

When y = 0, $f (x) = f (x) f' (0) + f (0) f' (x)$

$\Rightarrow \frac{1}{2} f (x) = f' (x)$ [ $∵$ f(0) = 1]

Integrating both sides, we get $f (x) = e^{x / 2} \cdot C$

Now, $f (0) = 1 \Rightarrow f (x) = e^{x / 2} \Rightarrow \log_{e} f (x) = \frac{x}{2}$

$∴ \sum_{n = 1}^{100} \log_{e} f (n)$

$= \sum_{n = 1}^{100} \frac{n}{2} = \frac{1}{2} \frac{(100) (101)}{2} = 2525$ .

Q 38 :
If the function $f (x)$ $=$ ${\begin{matrix} \frac{2}{x} {\sin (k_{1} + 1) x + \sin (k_{2} - 1) x}, & x < 0 \\ 4, & x = 0 \\ \frac{2}{x} \log_{e} (\frac{2 + k_{1} x}{2 + k_{2} x}), & x > 0 \end{matrix}$ is continuous at x = 0, then $k_{1}^{2} + k_{2}^{2}$ is equal to [2025]

20
5
10
8

1

2

3

4

(3)

$\lim_{x \to 0^{-}} f (x) = \lim_{x \to 0} \frac{2}{x} {\sin (k_{1} + 1) x + \sin (k_{2} - 1) x} = 4$

$\Rightarrow 2 (k_{1} + 1) + 2 (k_{2} - 1) = 4$

$\Rightarrow 2 [k_{1} + 1 + k_{2} - 1] = 4$

$\Rightarrow k_{1} + k_{2} = 2$ ... (i)

$\lim_{x \to 0^{+}} f (x) = \lim_{x \to 0} \frac{2}{x} \log_{e} (\frac{2 + k_{1} x}{2 + k_{2} x}) = 4$

$\lim_{x \to 0^{+}} \frac{1}{x} \log_{e} (\frac{2 + k_{1} x}{2 + k_{2} x}) = 2$ ;

$\lim_{x \to 0^{+}} \frac{1}{x} \log_{e} (1 + \frac{(k_{1} - k_{2}) x}{2 + k_{2} x}) = 2$

$\Rightarrow \frac{k_{1} - k_{2}}{2} = 2 \Rightarrow k_{1} - k_{2} = 4$ ... (ii)

Adding (i) and (ii), we get

$k_{1} = 3 \Rightarrow k_{2} = - 1$

$∴ k_{1}^{2} + k_{2}^{2} = {(3)}^{2} + {(- 1)}^{2} = 9 + 1 = 10$ .

Q 39 :
Let [x] denote the greatest integer function, and let m and n respectively be the numbers of the points, where the function $f (x) = [x] + | x - 2 |, - 2 < x < 3$ , is not continuous and not differentiable Then m + n is equal to : [2025]

7
8
6
9

1

2

3

4

(2)

Given : $f (x) = [x] + | x - 2 |, - 2 < x < 3$

The function can also be written as follows:

$f (x)$ $=$ ${\begin{matrix} - x, & - 2 < x < - 1 \\ - x + 1, & - 1 \leq x < 0 \\ - x + 2, & 0 \leq x < 1 \\ - x + 3, & 1 \leq x < 2 \\ x, & 2 \leq x < 3 \end{matrix}$

Here, function f(x) is not continuous at x = –1, 0, 1 and 2.

Hence, function f(x) is not differentiable at x = –1, 0, 1 and 2.

So, we have m = n = 4.

$∴$ m + n = 4 + 4 = 8.

Q 40 :
Let the function $f (x) = (x^{2} - 1) | x^{2} - a x + 2 | + \cos | x |$ be not differentiable at the two points $x = α = 2$ and $x = β$ . Then the distance of the point $(α, β)$ from the line 12x + 5y +10 = 0 is equal to : [2025]

4
3
2
5

1

2

3

4

(*)

We have,

$f (x) = (x^{2} - 1) | x^{2} - a x + 2 | + \cos | x |$

Now, cos |x| is always differentiable

So, we will check for $| x^{2} - a x + 2 |$ and it is not differentiable at its roots.

It is given that $x = α = 2$

$\Rightarrow {(2)}^{2} - a (2) + 2 = 0 \Rightarrow 4 - 2 a + 2 = 0 \Rightarrow a = 3$

The other root of $x^{2} - 3 x + 2 is x = 1$ .

Note: There is error in question, f(x) is differentiable at x = 1.

Topic Question Set

Q 31 :
Consider the function $f : (0, \infty) \to R$ defined by $f (x) = e^{- | \log_{e} x |}$ . If $m$ and $n$ be respectively the number of points at which $f$ is not continuous and $f$ is not differentiable, then $m + n$ is [2024]

Q 32 :
Let $f (x) = 2^{x} - x^{2}, x \in R .$ If $m$ and $n$ are respectively the number of points at which the curves $y = f (x)$ and $y = f' (x)$ intersect the $x -$ axis, then the value of $m + n$ is _________. [2024]

0%

Q 33 :
Let $f : R \to R$ be a twice differentiale function such that (sin x cos y)(f(2x + 2y) – f(2x – 2y)) = (cos x sin y)(f(2x + 2y) + f(2x – 2y)), for all x, y $\in$ R.

If $f' (0) = \frac{1}{2}$ , then the value of $24 f'' (\frac{5 π}{3})$ is : [2025]

Q 34 :
Let $f (x)$ $= {\begin{matrix} {(1 + a x)}^{1 / x}, & x < 0 \\ 1 + b, & x = 0 \\ \frac{{(x + 4)}^{1 / 2} - 2}{{(x + c)}^{1 / 3} - 2} & x > 0 \end{matrix} \begin{matrix} \end{matrix}$ be continuous at x = 0. Then $e^{a} b c$ is equal to : [2025]

Q 35 :
If $y (x)$ $=$ $| \begin{matrix} \sin x & \cos x & \sin x + \cos x + 1 \\ 27 & 28 & 27 \\ 1 & 1 & 1 \end{matrix} |$ $, x \in ℝ$ , then $\frac{d^{2} y}{d x^{2}} + y$ is equal to [2025]

Q 36 :
Let $f : R \to R$ be a continuous function satisfying f(0) = 1 and f(2x) – f(x) = x for all x $\in$ R. If $\lim_{n \to \infty} {f (x) - f (\frac{x}{2^{n}})} = G (x)$ , then $\sum_{r = 1}^{10} G (r^{2})$ is equal to [2025]

Q 37 :
Let f(x) be a real differentiable function such that f(0) = 1 and $f (x + y) = f (x) f' (y) + f' (x) f (y)$ for all x, y $\in$ R. Then $\sum_{n = 1}^{100} \log_{e} f (n)$ is equal to : [2025]

Q 38 :
If the function $f (x)$ $=$ ${\begin{matrix} \frac{2}{x} {\sin (k_{1} + 1) x + \sin (k_{2} - 1) x}, & x < 0 \\ 4, & x = 0 \\ \frac{2}{x} \log_{e} (\frac{2 + k_{1} x}{2 + k_{2} x}), & x > 0 \end{matrix}$ is continuous at x = 0, then $k_{1}^{2} + k_{2}^{2}$ is equal to [2025]

Q 39 :
Let [x] denote the greatest integer function, and let m and n respectively be the numbers of the points, where the function $f (x) = [x] + | x - 2 |, - 2 < x < 3$ , is not continuous and not differentiable Then m + n is equal to : [2025]

Q 40 :
Let the function $f (x) = (x^{2} - 1) | x^{2} - a x + 2 | + \cos | x |$ be not differentiable at the two points $x = α = 2$ and $x = β$ . Then the distance of the point $(α, β)$ from the line 12x + 5y +10 = 0 is equal to : [2025]

Want Us to Email you About Special Offers & Updates?

Topic Question Set

Q 31 : Consider the function f:(0,∞)→R defined by f(x)=e-|logex|. If m and n be respectively the number of points at which f is not continuous and f is not differentiable, then m+n is [2024]

Q 32 : Let f(x)=2x-x2, x∈R. If m and n are respectively the number of points at which the curves y=f(x) and y=f'(x) intersect the x-axis, then the value of m+n is _________. [2024]

0%

Q 33 : Let f:R→R be a twice differentiale function such that (sin x cos y)(f(2x + 2y) – f(2x – 2y)) = (cos x sin y)(f(2x + 2y) + f(2x – 2y)), for all x, y ∈ R. If f'(0)=12, then the value of 24f''(5π3) is : [2025]

Q 34 : Let f(x)={(1+ax)1/x,x<01+b,x=0(x+4)1/2–2(x+c)1/3–2x>0 be continuous at x = 0. Then eabc is equal to : [2025]

Q 35 : If y(x)=|sinxcosxsinx+cosx+1272827111|, x∈ℝ, then d2ydx2+y is equal to [2025]

Q 36 : Let f:R→R be a continuous function satisfying f(0) = 1 and f(2x) – f(x) = x for all x∈ R. If limn→∞{f(x)–f(x2n)}=G(x), then ∑r=110G(r2) is equal to [2025]

Q 37 : Let f(x) be a real differentiable function such that f(0) = 1 and f(x+y)=f(x)f'(y)+f'(x)f(y) for all x, y ∈ R. Then ∑n=1100loge f(n) is equal to : [2025]

Q 38 : If the function f(x)={2x{sin(k1+1)x+sin(k2–1)x},x<04, x=02xloge(2+k1x2+k2x),x>0 is continuous at x = 0, then k12+k22 is equal to [2025]

Q 39 : Let [x] denote the greatest integer function, and let m and n respectively be the numbers of the points, where the function f(x)=[x]+|x–2|,–2<x<3, is not continuous and not differentiable Then m + n is equal to : [2025]

Q 40 : Let the function f(x)=(x2–1)|x2–ax+2|+cos|x| be not differentiable at the two points x=α=2 and x=β. Then the distance of the point (α, β) from the line 12x + 5y +10 = 0 is equal to : [2025]

Want Us to Email you About Special Offers & Updates?

Q 31 :
Consider the function $f : (0, \infty) \to R$ defined by $f (x) = e^{- | \log_{e} x |}$ . If $m$ and $n$ be respectively the number of points at which $f$ is not continuous and $f$ is not differentiable, then $m + n$ is [2024]

Q 32 :
Let $f (x) = 2^{x} - x^{2}, x \in R .$ If $m$ and $n$ are respectively the number of points at which the curves $y = f (x)$ and $y = f' (x)$ intersect the $x -$ axis, then the value of $m + n$ is _________. [2024]

Q 33 :
Let $f : R \to R$ be a twice differentiale function such that (sin x cos y)(f(2x + 2y) – f(2x – 2y)) = (cos x sin y)(f(2x + 2y) + f(2x – 2y)), for all x, y $\in$ R.

If $f' (0) = \frac{1}{2}$ , then the value of $24 f'' (\frac{5 π}{3})$ is : [2025]

Q 34 :
Let $f (x)$ $= {\begin{matrix} {(1 + a x)}^{1 / x}, & x < 0 \\ 1 + b, & x = 0 \\ \frac{{(x + 4)}^{1 / 2} - 2}{{(x + c)}^{1 / 3} - 2} & x > 0 \end{matrix} \begin{matrix} \end{matrix}$ be continuous at x = 0. Then $e^{a} b c$ is equal to : [2025]

Q 35 :
If $y (x)$ $=$ $| \begin{matrix} \sin x & \cos x & \sin x + \cos x + 1 \\ 27 & 28 & 27 \\ 1 & 1 & 1 \end{matrix} |$ $, x \in ℝ$ , then $\frac{d^{2} y}{d x^{2}} + y$ is equal to [2025]

Q 36 :
Let $f : R \to R$ be a continuous function satisfying f(0) = 1 and f(2x) – f(x) = x for all x $\in$ R. If $\lim_{n \to \infty} {f (x) - f (\frac{x}{2^{n}})} = G (x)$ , then $\sum_{r = 1}^{10} G (r^{2})$ is equal to [2025]

Q 37 :
Let f(x) be a real differentiable function such that f(0) = 1 and $f (x + y) = f (x) f' (y) + f' (x) f (y)$ for all x, y $\in$ R. Then $\sum_{n = 1}^{100} \log_{e} f (n)$ is equal to : [2025]

Q 38 :
If the function $f (x)$ $=$ ${\begin{matrix} \frac{2}{x} {\sin (k_{1} + 1) x + \sin (k_{2} - 1) x}, & x < 0 \\ 4, & x = 0 \\ \frac{2}{x} \log_{e} (\frac{2 + k_{1} x}{2 + k_{2} x}), & x > 0 \end{matrix}$ is continuous at x = 0, then $k_{1}^{2} + k_{2}^{2}$ is equal to [2025]

Q 39 :
Let [x] denote the greatest integer function, and let m and n respectively be the numbers of the points, where the function $f (x) = [x] + | x - 2 |, - 2 < x < 3$ , is not continuous and not differentiable Then m + n is equal to : [2025]

Q 40 :
Let the function $f (x) = (x^{2} - 1) | x^{2} - a x + 2 | + \cos | x |$ be not differentiable at the two points $x = α = 2$ and $x = β$ . Then the distance of the point $(α, β)$ from the line 12x + 5y +10 = 0 is equal to : [2025]