Topic Question Set
Q 11
:
The area enclosed by the curves and is equal to: [2024]
(4)
We have,
For intersecting points:
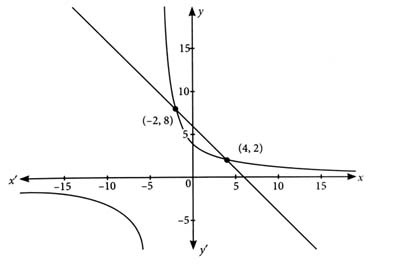
So,
Q 12
:
The area (in square units) of the region bounded by the parabola and the line is [2024]
9
7
8
6
(1)
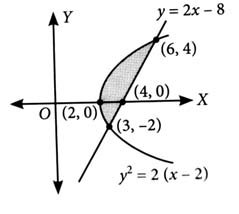
Parabola : ...(i)
and line : ...(ii)
From (ii), we get
Points of intersection of (i) and (ii) are and
Q 13
:
The area of the region
is [2024]
(1)
The area of region
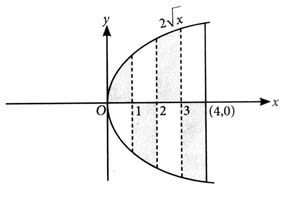
Case 1:
So,
Case 2:
So,
Q 14
:
The area of the region enclosed by the parabolas and is equal to [2024]
6
4
-
-
(1)
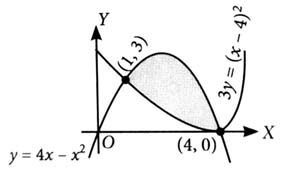
Given, ...(i)
...(ii)
From (i),
From (ii),
Points of intersection are and
Required area =
Q 15
:
The area of the region enclosed by the parabolas and is ___________ [2024]
(72)
Given, and
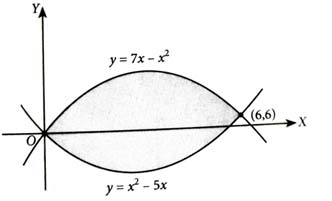
Both curves passes through the origin
For the points of intersection, we have
Area bounded by the curves
Q 16
:
Let the area of the region enclosed by the curve and the -axis between to be Then is equal to ______ . [2024]
(16)
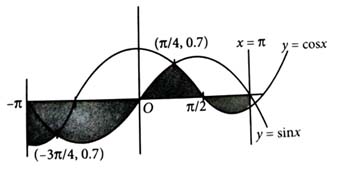
Required area,
Q 17
:
Let the area of the region be where and are coprime numbers. Then is equal to _____ . [2024]
(119)
Given, ...(i)
...(ii)
...(iii)
The point intersection of (i) and (iii) are and
The point of intersection of (i) and (ii) are and
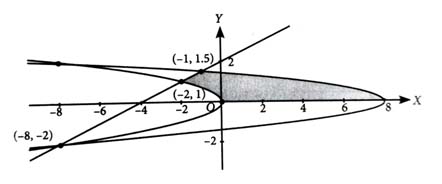
Required area
Q 18
:
If the area of the region is then 12A is equal to ____________. [2024]
(304)
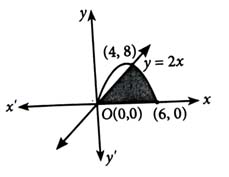
Region
Let A be the area of the required region.
Q 19
:
The area (in sq. units) of the part of the circle which is below the line is where are coprime numbers. Then is equal to _______ . [2024]
(171)
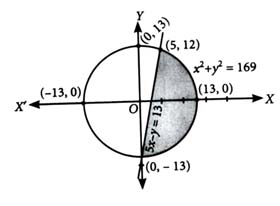
Q 20
:
Let the area of the region be Then 12A is equal to ___________ . [2024]
(164)
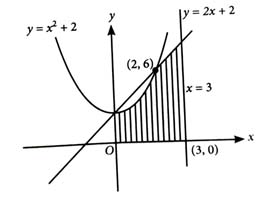
Required area,

