The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
5 units
12 units
11 units
units
(2) 12 units
Assertion (A): The value of y is 3, if the distance between the points P(2, -3) and Q(10, y) is 10.
Reason (R): Distance between two points is given by
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of Assertion (A)
Assertion (A) is true but reason (R) is false.
Assertion (A) is false but reason (R) is true.
(1)
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
AD is a median of ABC with vertices A(5, –6), B(6, 4) and C(O, O). Length AD is equal to :
units
units
units
10 units
(1)
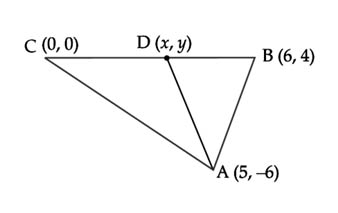
Using the mid point formula, the coordinates of mid-point of BC are
Co-ordinates of
Now, length of
If the distance between the points (3, –5) and (x, –5) is 15 units, then the values of x are :
12, –18
–12, 18
18, 5
–9, –12
(2)
If the vertices of a parallelogram PQRS taken in order are P(3, 4), Q(-2, 3) and R(-3, -2), then the coordinates of its fourth vertex S are
(-2, -1)
(-2, -3)
(2, -1)
(1, 2)
(3)
We know that the diagonals of a parallelogram bisect each other.
Therefore, midpoint of QS = midpoint of PR. Let the coordinate of S is (x, y)
Hence, fourth vertex S are (2, -1).
The centre of a circle is at (2, 0). If one end of a diameter is at (6, 0), then the other end is at :
(0, 0)
(4, 0)
(-2, 0)
(-6, 0)
(3)
⇒ x = –2 and y = 0
Assertion (A): If the co-ordinates of the mid-points of the sides AB and AC of are D(3,5) and E(-3,-3) respectively, then BC = 20 units
Reason (R) : The line joining the mid points of two sides of a triangle is parallel to the third side and equal to half of it.
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A)
Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A)
Assertion (A) is true but reason (R) is false.
Assertion (A) is false but reason (R) is true.
(1)
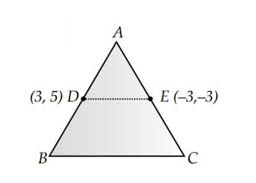
For assertion : Distance between two points and
Distance between
By midpoint theorem, distance between
So, assertion is true.
For reason: By midpoint theorem, the line joining the mid points of two sides of a triangle is parallel to the third side and equal to half of it. So, reason is also true.
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A)
XOYZ is a rectangle with vertices X(–3, 0), O(0, 0), Y(0, 4) and Z(x, y). The length of its each diagonal is
units
units
units
units
(1)
We know that, Length of Diagonals are equal
In Rectangle, ZO = YX
The point on x-axis which is equidistant from the points (5, – 3) and (4, 2) is :
(4.5, 0)
(7, 0)
(0.5, 0)
(– 7, 0)
(2) (7, 0)
PQ is a diameter of a circle with centre O(2, – 4). If the coordinates of the point P are (– 4, 5), then the coordinates of the point Q will be :
(– 3, 4.5)
(– 1, 0.5)
(4, – 5)
(8, – 13)
(4) (8, – 13)